A. MP3 Player
Xotira: 32 MB, Vaqt: 1000 msKomiljon musiqani eshitishni yoqtiradi. Ammo uning telefonidagi musiqa dasturi g‘alati ishlaydi. Komiljonning telefonidagi mp3 player shunday tuzilganki, agar foydalanuvchi hozirda \(K\)-musiqani eshitayotgan bo‘lsa, maxsus tugmalarni bosish orqali u \(K + 1\), \(K - 1\), \(K + 2\), \(K - 2\) musiqalardan biriga o‘tishi mumkin.
Komiljon hozir \(X\)-musiqani tinglamoqda, lekin u do‘sti Adhambekka \(Y\)-musiqani namoyish etmoqchi. U buni amalga oshirish uchun kamida necha marta maxsus tugmalardan foydalanishi kerak ekanligi toping.
Kirish oqimining birinchi qatorida bitta butun son - \(X(1 \leq X \leq 500)\) Komiljon hozir tinglayotgan musiqa tartib raqami kiritiladi.
Kirish oqimining ikkinchi qatorida bitta butun son - \(Y(1 \leq Y \leq 500)\) Komiljon do‘sti Adhambekka namoyish etmoqchi bo‘lgan musiqa tartib raqami kiritialdi.
Masala javobini ekranga chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 6 |
1 |
B. Tubga bo'linmas
Xotira: 32 MB, Vaqt: 1000 msSizga \(N(1 \leq N \leq 300)\) soni beriladi. 1 dan farqli shunday eng kichik natural sonni topingki, u birinchi \(N\) ta tub songa bo‘linmasin.
1 va o‘zidan farqli bo‘luvchisiga ega bo‘lmagan son tub son hisoblanadi. 19 va 2 sonlari tub sonlar hisoblanadi, 49 va 4 sonlari esa tub emas.
Kirish oqimining birinchi qatorida bitta butun son - \(N\) soni kiritiladi.
Masala javobini ekranga chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 |
11 |
C. Olma uzish
Xotira: 64 MB, Vaqt: 1000 msKomiljon va uning do‘stlarining jami \(N\) kishilik do‘stlar davrasini tashkil qiladi. \(i\)-bolada \(A_i\) ta olma bor. Agar barcha bolada bir xil sondagi olmalar bo‘lmasa kimdir xafa bo‘lishi mumkin. Shuning uchun ham har bir bola bog‘dagi daraxtga bir marta chiqib o‘zidan tashqari barcha do‘stlariga bittadan olma uzib tushishi mumkin. Hech kim xafa bo‘lmasligi uchun daraxtga kamida necha marta chiqib tushishga to‘g‘ri keladi?
Kirish oqimining birinchi qatorida bitta butun son - \(N(1 \leq N \leq 2 \cdot 10^5)\) jami bolalar soni kiritiladi.
Kirish oqimining ikkinchi qatorida probel bilan ajratilgan \(N\) ta butun son - \(A_i(1 \leq A_i \leq 10^9)\) \(i\) - boladagi olmalar soni kiritiladi.
Daraxtga chiqib tushishlar minimal sonini chiqaring.
1-testda: 1-bola 1 marta, 3-bola 2 marta daraxtga chiqib tushishi kerak.
2-testda: barcha bolalarda olmalar soni teng.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 2 1 3 |
3 |
| 2 |
2 1 1 |
0 |
D. Binar satr
Xotira: 256 MB, Vaqt: 1500 ms\(S\) binar satr berilgan. \(F(l, r)\) deb \(S[l ..r]\)qism satrning lik sanoq sistemasidagi qiymatiga aytiladi. \(S\) satrning uzunligi \(N\) bo‘lsa, barcha \(N(N+1) \over 2\) ta \(F(l, r)\) qiymatlari ichidan mavjud bo‘lmagan eng kichik nomanfiy butun sonni toping.
Kirish oqimida yagona qatorda \(S\) satr kiritiladi. \((1 \le |S| \le 2 \cdot 10^5)\)
Barcha \(F(l, r)\) qiymatlarning orasida mavjud bo‘lmagan eng kichik nomanfiy butun sonni chiqaring.
1-testda: \(F(l, r)\) qiymatlar ichida \(0_2=0\); \(1_2=1\); \(10_2=2\); \(11_2 = 3\); \(100_2=4\) sonlari mavjud. Ammo \(101_2=5\) mavjud emas. Demak, javob 5.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
100110 |
5 |
| 2 |
1111 |
0 |
E. Mamlakatlar va shaharlar
Xotira: 256 MB, Vaqt: 2000 ms\(K\)ta mamlakatda jami \(N\)ta shahar bor. Birinchi mamlakatda \(a_1\)ta, ikkinchi mamlakatda \(a_2\)ta, \(K\)-mamlakatda \(a_K\)ta shahar bor va ular ketma-ket raqamlangan. Xususan:
1-mamlakat shaharlari \(1\)dan \(a_1\)gacha;
2-mamlakat shaharlari \(a_1+1\)dan \(a_1+a_2\)gacha;
…
K-mamlakat shaharlari \(a_1+a_2+...+a_{K-1} + 1\)dan \(N\)gacha.
Shaharlar orasida harakatlanish uchun yo‘llar qurilgan. Bunda ixtiyoriy \(1 \leq i < N\) uchun \(i\) va \(i+1\)-shaharlar o‘rtasida yo‘l bor. Undan tashqari, \(M\)ta qo‘shimcha yo‘l bir mamlakat ichidagi ikkita shaharni bog‘lab turadi.
Sizga \(Q\)ta so‘rovda har xil mamlakatda joylashgan \(X\) va \(Y\) shaharlar beriladi. Vazifangiz \(X\) shahardan \(Y\) shaharga boruvchi eng qisqa yo‘llar sonini topish. Javob katta bo‘lib ketishi mumkinligi sababli, javobni \(10^9+7\)ga bo‘lgandagi qoldig‘ini chiqaring.
Birinchi qatorda uchta butun son - \(K, N, M\) sonlari kiritiladi. \((1 \le K, N, M \le 3 \cdot 10^5; K \le N)\)
Ikkinchi qatorda \(a_1,a_2,...,a_K\) beriladi. \((a_i \ge 1; a_1+a_2+...+a_K=N)\)
Keyingi \(M\)ta qatorning har birida ikkitadan butun son - \(u\) va \(v\) beriladi, bu \(u\) va \(v\) shaharlar o‘rtasida qo‘shimcha yo‘l borligini anglatadi. \((1 \le u, v \le N; |u-v| \ge 2)\). Qo‘shimcha yo‘llar bog‘lovchi shaharlar bitta davlatda joylashganligi kafolatlanadi.
Keyingi qatorda bitta butun son \(Q\) beriladi. \((1 \le Q \le 3 \cdot 10^5)\)
Keyingi \(Q\)ta qatorda \(X\) va \(Y\) shaharlar beriladi. \((1 \le X, Y \le N)\). Bunda ular har xil mamlakatda ekanligi kafolatlanadi.
Har bir so‘rov uchun bitta yangi qatorda so‘rovlarga javobni \(10^9+7\)ga bo‘lingandagi qoldig‘ini chiqaring.
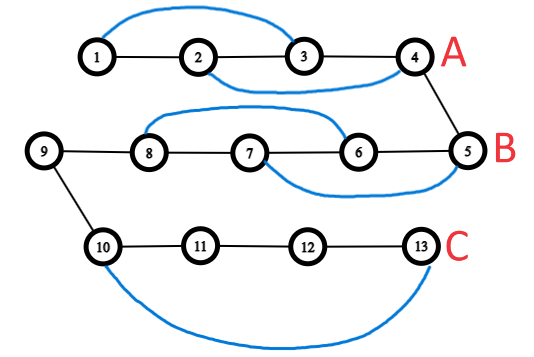
Rasmda 3ta mamlakat va 13ta shahar bor. 1, 2, 3-shaharlar A mamlakatga; 4, 5, 6, 7, 8, 9-shaharlar B mamlakatga va 10, 11, 12, 13-shaharlar C mamlakatga tegishli. Shuningdek 1-3, 2-4, 5-7, 6-8, hamda 10-13 shaharlar o‘rtasida qo‘shimcha yo‘llar mavjud.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 13 5 4 5 4 1 3 4 2 8 6 10 13 5 7 3 7 12 4 5 1 13 |
2 1 4 |