A. Uddalab bo'lmas topshiriq
Xotira: 32 MB, Vaqt: 1000 msBir kuni Shohruhga domla bir masala berdi. U matematikani juda zo'r bilardi, ammo, bu masalada qiynaldi. Masala quyidagicha edi:
\(F\) funksiyani \(N\)-hadini topish uchun quyidagicha ish bajarish kerak edi:
\(F(0) = 1+3*0+3*0*0=1\)
\(…\)
\(F(n) = 1+3*n+3*n*n\)
Sizga N butun soni berilgan. Siz esa quyidagi \(F(0)+F(1)+F(2)+…+F(n)\) yig'indini hisoblashingiz kerak.
Bitta qatorda \(N\) butun soni \(N(0≤N≤10^9).\)
Yagona qatorda masala yechimi \(10^9+7 \)ga bo'lgandagi qodiqni chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 |
8 |
| 2 |
0 |
1 |
B. Guruhlash
Xotira: 32 MB, Vaqt: 1000 msSizda har birida \(2^i\) tadan odam bo'lgan \(A_i\) ta guruh bor. \((0 \le i \le N)\) (To'liqroq tushunish uchun izohga qarang).
Siz odamlarni bir nechta xonalarga joylashtirishingiz zarur. Bu uchun quyidagi shartlar bajarilishi kerak:
- Har bir xonada \(2^N\) tadan odam bo'lishi kerak.
- Bir guruhdagi odamlar bitta xonada bo'lishi kerak.
Nechta xona kerakligini yoki bu ish imkonsizligini aniqlang.
Birinchi qatorda \(N(0 \le N \le 30)\) soni kiritiladi.
Keyingi qatorda N+1 ta butun son - A massiv elementlari kiritiladi. \((0 \le A_i \le 10^9)\)
Kerakli xonalar sonini chop eting. Agar xonalarga joylashtirishning iloji bo'lmasa -1 ni chop eting.
1-test: a, b, c, d harflarini 1, 2, 4 va 8 kishilik guruhlar deb tasavvur qilamiz. Quyidagicha joylashtirish mumkin: {a,a,a,a,b,b}, {d}, va {d}.
2-test uchun xonalarga joylash imkonsiz.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 4 2 0 2 |
3 |
| 2 |
1 3 0 |
-1 |
C. Deyarli tub sonlar
Xotira: 128 MB, Vaqt: 2000 msSiz matematikadan tub son degan tushunchani bilsangiz kerak. Yana shunday sonlar borki ular tub bo'lishi uchun bo'luvchilari soni \(1\) taga ko'payib ketgan. Biz esa bunday sonlarni deyarli tub sonlar deymiz. Misol uchun \(4\) soni deyarli tub son chunki uning bo'luvchilari soni \(3\) ta yani \([1,2,4]\). Misol uchun \(5\) soni deyarli tub son emas chunki uning natural bo'luvchilari soni \(2\) ta ya'ni \( [1,5]\). Sizga bu masala \(T\) ta so'rov berilgan. Har bir so'rovga alohida javob chiqarishingiz kerak bo'ladi. Har bir so'rovda \(L\) va \(R\) sonlari beriladi siz \(L\) va \(R\) oralig'idagi deyarli tub sonlar sonini chiqarishingiz kerak bo'ladi.
Birinchi qatorda bitta butun \(T\) soni \(T(1≤T≤10^5).\)
Keyingi \(T\) ta qatorda \(L\) va \(R\) butun sonlari \(L,R(1≤L≤R≤10^{12}).\)
Har bitta so'rovga javoblarni chiqaring.
\(1\)-testni ko'rib chiqsak.
\(1\) va \(10\) oralig'idagi deyarli tub sonlar \([4,9]\) lar ya'ni \(2\) ta
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 1 10 |
2 |
D. Sobirjon qiziqqan matritsa
Xotira: 128 MB, Vaqt: 1000 msDo`stimiz Sobirjon \(NxM\) (\(N\) ga \(N\) lik) matritsalarni juda yoqtiradi. Matritsalarga doir masala ishlab o`tirgan paytida, u shuni o`ylab qoldiki, agar L uzunlikdagi massiv berigan bo`lsa, necha xil usulda uni, \(NxM\) matritsaga aylantirish mumkin?🤔
Sobirjon bu masalani yechishda biroz qiynalyapti, va u sizdan yordam so`ramoqchi. Unga yordam bera olasizmi?
INPUT.TXT kirish faylida yagona butun son, \(L(0 \le L\le 10^{14})\) soni kiritiladi.
OUTPUT.TXT faylining birinchi qatorida shartlarni qanoatlantiradigan N va M lar sonini, keyingi qatorlarda esa, N va M sonlarini o`sib borish tartibida chiqaring. Agar bunday sonlar mavjud bo`lmasa, 0 ni chiqaring.
1-testda 2ta bo`lishi mumkin bo`lga holat mavjud.
Eslatma: (1xM) yoki (Nx1) lar matritsa bo`la olmaydi deb hisoblansin!
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
8 |
2 2 4 4 2 |
E. Sayohat - 1
Xotira: 256 MB, Vaqt: 2000 msRobolandiya davlatida noodatiy dengiz borligi aniqlandi. Bu dengizning ba'zi qismlarida orollar mavjud. Ushbu dengizning xaritasini 0 dan N-1 gacha raqamlangan qator va 0 dan M-1 gacha raqamlangan ustunlardan tashkil topgan \(N*M\) matritsa ko'rinishida tasvirlash mumkin. \((i, j)\) katakcha uchun agar \(i \& j == 0\) (& - bitwise and operatori) bo'lsa - quruqlik, aks holda dengiz hisoblanadi.
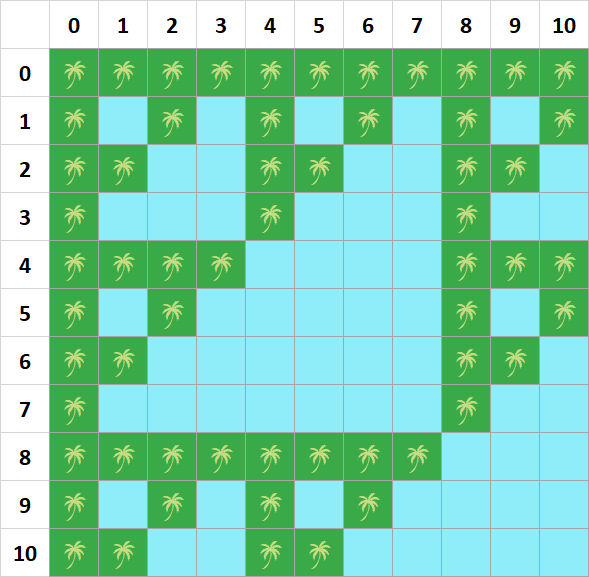
Siz ushbu dengizdagi orollarda sayohat qilishni xohlaysiz. Sizda dron va velosiped bor. Dron yordamida istalgan oroldan boshqasiga borish mumkin, velosiped yordamida esa faqat qo'shni orolga o'tish mumkin.
A, B, C, va D sonlari berilgan bo'lsa \([A, C]\) oralig'idagi qator va \([B, D]\) oralig'idagi ustun orasida joylashgan orollarning har birini aylanib chiqish uchun kamida necha marta drondan foydalanish zarur?
Birinchi qatorida N va M \((1 \le N, M \le 500)\) kiritiladi.
Keyingi qatorda A, B, C, D sonlari kiritiladi \((0 \le A \le C \le N-1)\)
\((1 \le B \le D \le M-1)\).
Belgilangan qismni aylanib chiqish uchun drondan necha marta foydalanilganini chop eting.
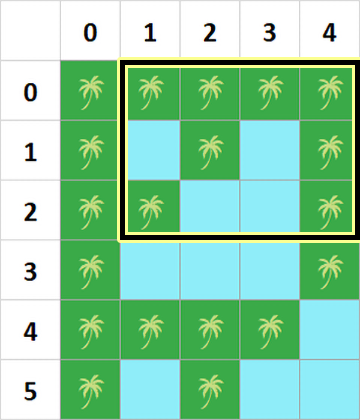
drondan foydalangan holda (0, 3) katakka tushamiz. U yerdan (2, 1) oroldan boshqa barcha orollarni velosiped yordamida aylanamiz. (2, 1) orolga dron orqali o'tamiz. Umumiy 2 marta drondan foydalandik.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 5 0 1 2 4 |
2 |
F. Ikkilik muvozanat
Xotira: 128 MB, Vaqt: 1000 msBir kuni Odiljon ismli bola yo'lda ketayotganda \(9\) sonini topib oldi. Keyin maktabda informatika darsida sanoq sistemalari mavzusini o'tgani esiga tushib qoldi. Shunda u \(9\) sonini ikkilik sanoq sistemasiga o'tkazdi. \(9_{10}->1001_2\). Qarasaki no'llar soni birlar soniga teng bo'lib qolipti. Keyin u \(N\) va \(M\) (\(N\) ham \(M\) ham kiradi) sonlari orasida ikkilik sanoq sistemasida no'llar soni birlar soniga teng bo'lgan sonlar soni nechtaligiga qiziqib qoldi. Dastlab u buni qo'lda hisoblamoqchi bo'ldi, lekin sonlar kattalashganda hisoblashga qiynalib qoldi. Siz unga dastur tuzib yordam bering.
Birinchi qatorda ikkita natural son \(N,M(1≤N<M≤10^{18})\)
Yagona qatorda masala javobini \(10^9+7\) ga bo'lgandagi qoldiqni chop eting
Birinchi testni ko'rib chiqamiz!
\([1,... ,10]\) oralig'ida \([2,9,10]\) larni birlar soni no'llar soniga teng.
\(2 -> 10\), \(1\)ta bir va \(1\)ta no'l bor.
\(9 -> 1001\),\(2\)ta bir va \(2 \)ta no'l bor.
\(10 -> 1010\),\(2\)ta bir va \(2\)ta no'l bor.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 10 |
3 |
G. Oxirgi yig'indi
Xotira: 256 MB, Vaqt: 2000 msBu masalada sizga \(N\) o'lchamli \(A\) massiv berilgan. Siz esa uni oxirgi elementi qolguncha quyidagi amalni bajarishingiz kerak bo'ladi. Misol uchun sizga 5 ta elementdan iborat quyidagi massiv berilsa\( [1,2,3,4,5]. [1+2,2+3,3+4,4+5]\) va keyin\( [3,5,7,9] \)massivi hosil qilinadi. So'ng yana\( [3+5,5+7,7+9] = [8,12,16]\). Bu amal toki massiv elementi bitta qolguncha davom etadi. \([8+12,12+16] = [20,28]\) va oxirida \([20+28]\) qoladi. Shunda natija \(48\)teng bo'ladi. Siz ham sizga berilgan massivni oxirgi elementi qolguncha shu amallarni ketma - ket bajarib borasiz. Eng oxirida qolgan elementni ekranga chiqarishingiz kerak bo'ladi.
Birinchi qatorda \(N\) soni \(N(3≤N≤10^6).\)
Ikkinchi qatorda \(N \) ta sondan iborat \(A\) massiv \(A[i] (1≤ A[i]≤10^9).\)
Yagona qatorda masala yechimini ekranga chiqaring.
Masala yechimi juda katta bo'lib ketishi mumkin shuning uchun uni \(10^9+7\) ga bo'lgandagi qoldiqni ekranga chiqarishingiz kerak bo'ladi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 1 2 3 4 5 |
48 |