A. Iftorlikga shokolad
Xotira: 32 MB, Vaqt: 1000 msDavlatbek va Asilbek ramazon oyida ro'za tutishgan. Ular iftorlik vaqti ingliz tili to'garagida bo'lishadi, og'iz ochar vaqtdan uyga qaytguncha kuch quvvat bo'lsin deb o'zlari bilan katakli shokolad olishgan. Davlatbekning shokoladi bo'yiga \(H_d\), eniga \(W_d\) kataklardan iborat. Asilbekning shokoladi esa bo'yiga \(H_a\), eniga \(W_a\) kataklardan iborat.
Ular to'garakda vaqtlari bilishdiki ramazon oyida faqatgina ular emas, to'garakdagi hamma ro'za tutgan ekan. Shunda ular iftorlik vaqtida o'zlarining shokoladlarini do'stlari bilan baham ko'rishga kelishib olishdi. Tasodifni qarangki agarda shokoladlarni \(1 \times 1\) o'lchamdagi katakchalarga bo'lishsa hammaga 1 tadan bo'lak nasib qilar ekan.
Kirish faylining yagona satrida to'rtta butun son, \(H_d, W_d, H_a, W_a (1 \le H_d, W_d, H_a, W_a \le 100)\) sonlari kiritiladi.
To'garakdagi jami bolalar sonini aniqlang!
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 5 8 5 |
60 |
B. Vaqt
Xotira: 32 MB, Vaqt: 1000 msSoniyalarda berilgan vaqtni namunadagi kabi soat, minut va sekundlarda chop eting.
Eslatma: 0 qiymatga ega ko'rsatkich chiqarilmasin!
Kirish faylining dastlabki satrida bitta natural son, soniyalarda ko'rsatilgan vaqt qiymati kiritiladi, qiymat \(10^5\) dan oshmasligi kafolotlanadi.
Soniyalarda berilgan vaqtning avval soat qiymatini, keyin daqiqa qiymatini so'ngra soniya qiymatini namunadagi singari chop eting!.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1000 |
16 daqiqa 40 soniya |
| 2 |
10000 |
2 soat 46 daqiqa 40 soniya |
| 3 |
3650 |
1 soat 50 soniya |
| 4 |
600 |
10 daqiqa |
C. G'alati idish
Xotira: 32 MB, Vaqt: 1000 msG'alati idish \(N\) qavatdan iborat bo'lib, uning \(i(1 \le i \le N)\)- qavati balandligi \(1\) sm va diametri \(D_i\) santimetrdan iborat silindrsimon shakldan iborat. Misol uchun \(D=\{7,6,4,3,7,2,5\}\) bo'lgan idishning umumiy ko'rinishi:
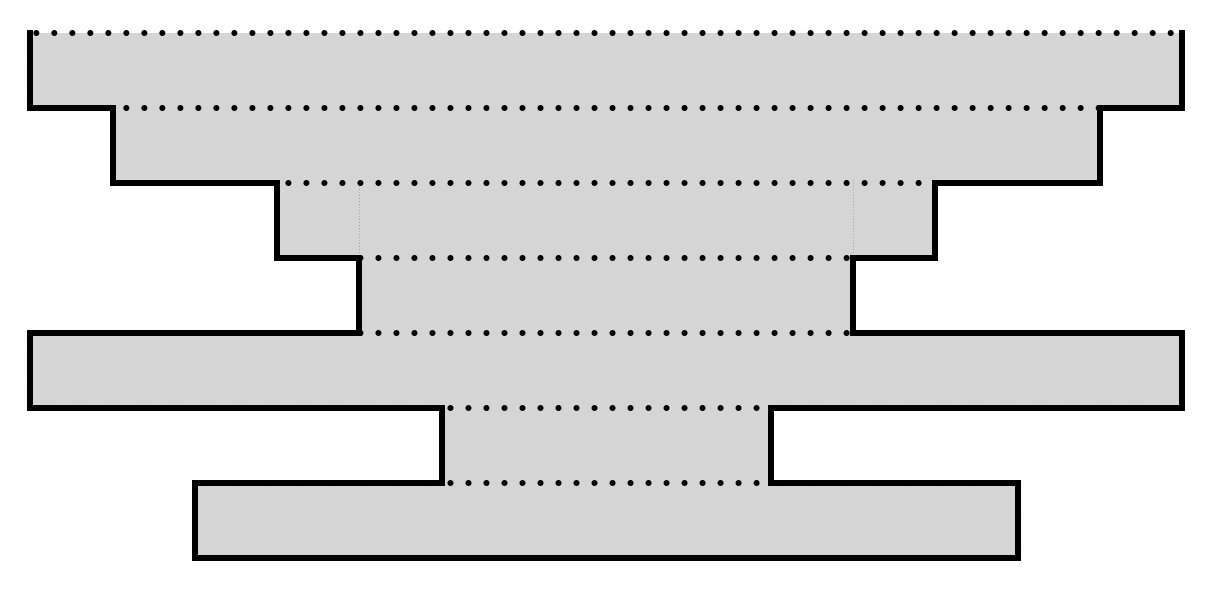
Eslatma: Idishning qavatlari yuqoridan - pastga yo'nalishida raqamlangan.
Siz idishning ichiga qalinligi \(1\) sm va diametri \(d_j (1 \le j \le M)\) bo'lgan jami \(M\) ta vaflini ketma-ket soldingiz. Misol uchun yuqorida ko'rsatilgan idishga \(d=\{3,2,5\}\) diametrli 3 ta vafli solgan bo'lsangiz idish quyidagicha ko'rinishda bo'ladi:
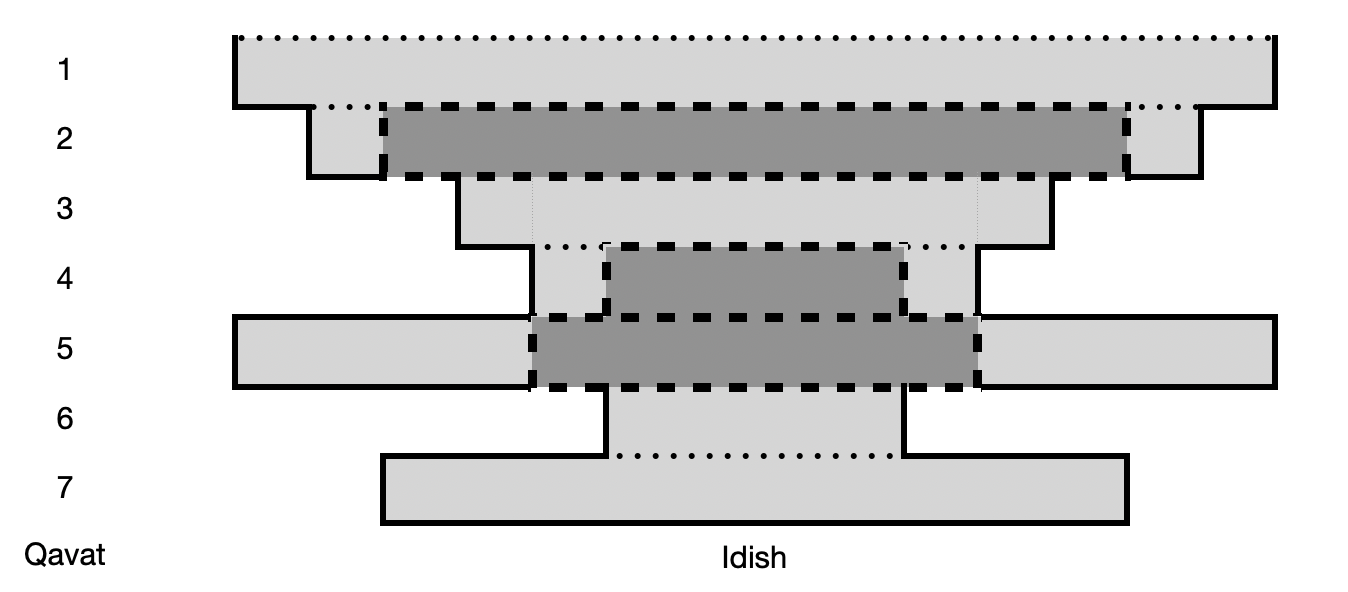
Kirish faylining dastlabki satrida \(N\) va \(M (1 \le N, M \le 300\ 000)\) sonlari, idishning balandligi hamda vaflilar soni kiritiladi.
Ikkinchi satrda bo'sh joy bilan ajratilgan holda \(N\) ta butun son, \(D_i (1 \le i \le N, 1 \le D_i \le 10^9)\)idishning har bir qavati diametri kiritiladi.
Uchinchi satrda bo'sh joy bilan ajratilgan holda \(M\) ta butun son, \(d_j (1 \le j \le M, 1 \le d_j \le 10^9)\) idishga solingan vaflilarning diametrlari idishga solinish ketma-ketligida kiritiladi.
Yagona butun son, idishga oxirgi solingan vafli agar idishni ichiga sig'masa 0 aks holda idishning qaysi qavatida joylashishini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
7 3 7 6 4 3 7 2 5 3 2 5 |
2 |
D. Palindrom sonlar
Xotira: 32 MB, Vaqt: 1000 msSon o'ngdan chapga va chapdan o'ngga yozilishi bir xil raqamlar ketma-ketligidan iborat bo'lsa palindrom son deyiladi.
\(N (1\le N \le 10^{18}) \) natural son berilgan.
Qiymati \(N\) dan kichik yoki teng bo'lgan nechta Natural palindrom son borligini chop eting!
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
7 |
7 |
| 2 |
57 |
14 |
| 3 |
88 |
17 |
E. Toshlar o'yini Pro Max
Xotira: 256 MB, Vaqt: 2000 msAnvar va Bobur yangi stol o'yinini o'ynashmoqda. Stolda \(N\)ta tosh bor. O'yin qoidalariga ko'ra \(K\) xil mumkin bo'lgan \(L[i], R[i]\) oraliqlar bor.
Navbati kelgan ishtirokchi stoldan bir-nechta toshlarni olishi kerak, bunda olingan toshlar soni mumkin bo'lgan ixtiyoriy oraliqqa tegishli bo'lishi kerak. Xususan, o'yinchi \(X\)ta tosh olishi uchun, qaysidir \(1 \le i \le K\) uchun \(L[i] \le X \le R[i]\) shart bajarilishi lozim. Yurish amalga oshira olmaydigan ishtirokchi o'yinda yutqazadi.
Agar o'yinni Anvar boshlasa va ikkala ishtirokchi ham optimal o'ynashsa, o'yinda kim g'alaba qozonadi?
Birinchi qatorda \(N\) va \(K\) sonlari beriladi. \((1 \le N \le 10^6)\) va \((1 \le K \le 100)\).
Keyingi \(K\)ta qatorda ikkitadan butun son, \(L[i]\) va \(R[i]\) beriladi. \((1 \le L[i] \le R[i] \le N)\).
Agar optimal o'yinda Anvar g'olib bo'lsa “Anvar”, aks holda “Bobur” deb chiqaring.
Birinchi misolda \(N=11\), berilgan oraliqlar \([1;3]\) va \([6; 7]\). Ya'ni bitta yurishda 1, 2, 3, 6, yoki 7ta tosh olish mumkin.
Anvarning strategiyasi birinchi yurishda 7ta tosh olish. Shunda stolda 4ta tosh qoladi. Shundan so'ng:
- Agar Bobur 1ta tosh olsa, Anvar 3ta tosh oladi va g'alaba qozonadi.
- Agar Bobur 2ta tosh olsa, Anvar 2ta tosh oladi va g'alaba qozonadi.
- Agar Bobur 3ta tosh olsa, Anvar 1ta tosh oladi va g'alaba qozonadi.
Demak, Boburning qanday o'ynashidan qat'iy nazar Anvarda yutish strategiyasi bor.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
11 2 1 3 6 7 |
Anvar |
| 2 |
20 1 3 6 |
Bobur |
F. Antiprime sonlar
Xotira: 32 MB, Vaqt: 1000 msOʻzidan kichik boʻlgan har qanday musbat sondan koʻproq natural boʻluvchiga ega boʻlgan musbat butun songa antiprime son deyiladi.
Misol uchun dastlabki antiprime sonlar quyidagilar: 1,2,4,6,12,24
Sizga \(N (1 \le N \le 2 \times 10^9)\)natural soni beriladi.
Qiymati \(N\) dan katta bo'lmagan eng katta antiprime sonni chop eting!
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1000 |
840 |
| 2 |
7 |
6 |
G. K-operatsiyasi
Xotira: 256 MB, Vaqt: 2000 msK-operatsiyasi, yohud Shurikning boshqa sarguzashtlari.
Ixtiyoriy \(C[1], C[2], ..., C[N]\) massivga k-operatsiyani qo'llaganda, u \(C[k+1], C[k+2], ..., C[N], C[k], C[k-1], ..., C[1]\) ko'rinishida o'zgaradi, bunda \(0 \le k < N\) shart bajarilishi kerak.
Sizga uzunliklari \(N\)ga teng bo'lgan \(A[1], A[2], ..., A[N]\) va \(B[1], B[2], ..., B[N]\) massivlar berilgan. Shuningdek, \(Q\)ta so'rovda \(l\) va \(r\) indekslar beriladi. Vazifangiz \(A[l], ..., A[r]\) oraliqda k-operatsiyalar qo'llab \(B[l],...,B[r]\) tenglashtirish mumkin yoki yo'qligini topish.
Birinchi qatorda \(N\) va \(Q\) butun sonlari beriladi, \((1 \le N, Q \le 2 \cdot 10^5)\).
Ikkinchi qatorda \(A[1], A[2], ..., A[N]\) beriladi, \((1 \le A[i] \le 10^9)\).
Uchinchi qatorda \(B[1], B[2], ..., B[N]\) beriladi, \((1 \le B[i] \le 10^9)\).
Keyingi \(Q\)ta qatorda \(l\) va \(r\) butun sonlari beriladi, \((1 \le l \le r \le N)\).
\(Q\)ta qatorda har bir so'rov uchun javobni chiqaring.
Birinchi so'rovda \(l=1\) va \(r=3\).
- \(k=1\) operatsiyani qo'llaymiz \(A=[2,1,3]\) → \(A = [1, 3, 2]\)
- \(k = 2\) operatsiyani qo'llaymiz \(A=[1,3,2]\) → \(A = [2,3,1]\)
Demak, javob YES.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 2 2 1 3 4 2 2 3 1 1 3 1 3 5 5 |
YES NO |