A. Hajm
Xotira: 16 MB, Vaqt: 1000 msAsosi 3 , 4 , 5 burchakli muntazam ko'pburchak bo'lgan piramidalar qiralar uzunliklari beriladi. Bu piramidalar muntazam ekanini inobatga olib barcha piramidalarni hajmlari yig'indisini toping.
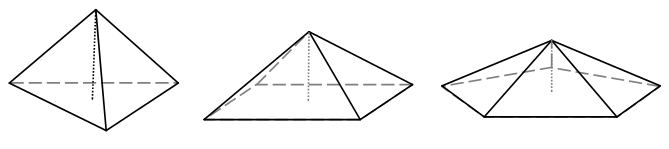
Kiritish faylida 1 - satrda piramidalar qiralar uzunliklari l1, l2, l3(1 ≤ l1, l2, l3 ≤ 1000) beriladi.
Chiqish faylida Piramidalar hajmlari yig'indisini chiqaring.
Yechim va sizning javobingiz orasidagi absolyut va nisbiy farq 10-9 dan oshmasin.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 5 3 |
38.546168065709 |
B. Archery World Club
Xotira: 16 MB, Vaqt: 1000 msQuvonchbek Play marketdan o'yin izlash paytida "Archery World Club 3D" o'yiniga ko'zi tushib yuklab olib o'ynab ko'rdi.
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ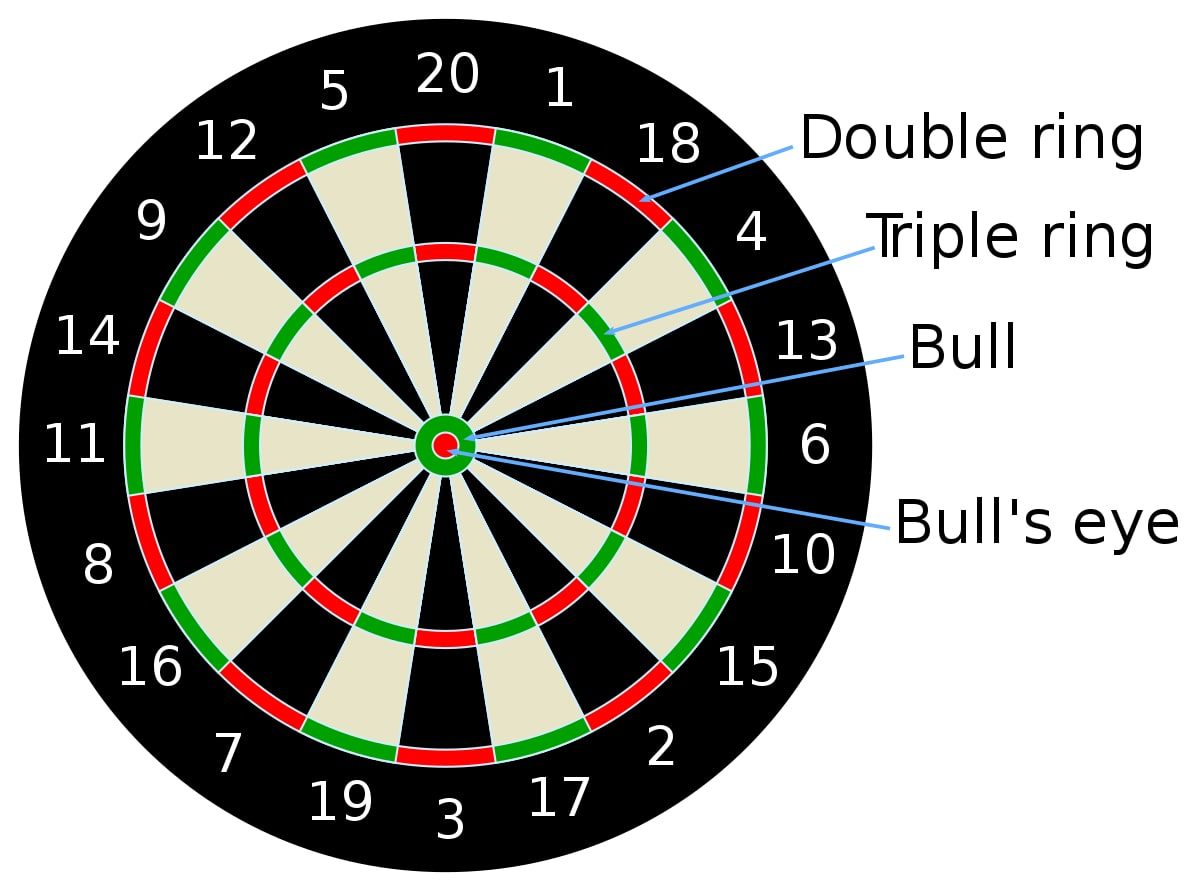
Bu o'yin shartlari shundan iborat o'yinda sizga dumoloq shaklida bo'yoqlardan iborat doska qandaydir uzoqlikda qo'yib beriladi, siz esa unga shu uzoqlikdan qancha aniqlikda urishingiz tekshiriladi. Quvonchbek esa bu o'yini o'ynab korib ajoyib ideyaga ega boldi, "Evrika, Evrika, Evrika... ". Quvonchbek o'yin shartlarini o'zgartirdi, topmoqchi bo'lgan narsa shundan iborat, dekart koordinatalar sistemasida istalgan nuqtani beradi va siz bu nuqta pastdagi chizmada qaysi rangda ekanligini aytishingiz kerak.
ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ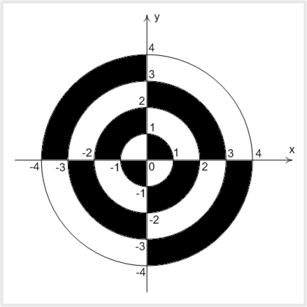
Kiritish faylida \(x, y (-1000 ≤ x,y ≤ 1000)\) 1 - qatorda probellar bilan ajratilgan holda kiritiladi.
Chiqish faylida berilgan koordinatalar qaysi rangda ekanligini chiqaring, oq rangli maydonlardan birida bolsa "oq" qora rangli maydonlardan biri bo'lsa "qora" chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
-4 4 |
qora |
| 2 |
4 4 |
oq |
C. Kvadrat va Kub sonlar
Xotira: 2 MB, Vaqt: 150 msSizga \(n\) natural soni beriladi. \(n\) gacha bo'lgan natural sonlar ichidan Kvadrat va Kub sonlar sonini nechta ekanligini topishingiz kerak.
Kiritish faylida 1 - qatorda testlar soni \(t(1≤t≤20)\) keyingi qatorlarda \(t\) ta son \(n(1≤n≤10^9)\) sonlar kiritiladi.
Chiqish faylida har bir test uchun alohida qatorlarda chop eting
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 1000 999 |
38 37 |
D. Uchburchaklar
Xotira: 16 MB, Vaqt: 1000 msMatematiklar yaxshi bilishadi uchburchak 3 ta tomon va 3 ta qiraga ega.Uchburchak tomonlarini ixtiyoriy belgilab boʻlmaydi. Ular quyidagi tengsizliklar bilan bogʻlangan (a, b, c uchburchak tomonlari):
- a + b > c
- a + c > b
- b + c > a
Yuqoridagi tengsizliklardan birortasi bajarilmagan holatda esa, uchburchak chala deb ataladi. Sizga \(a,b,c,d\) uzunlikdagi kesmalar beriladi. Siz bu kesmalardan foydalanib tomoni x, y, z( \(a ≤ x ≤ b ≤ y ≤ c ≤ z ≤ d\) ) bo'lgan uchburchaklarni nechata ekanini aniqlashingiz kerak.
Kiritish faylida 1- qatorda 4 ta butun son \(a,b,c,d (1 ≤ a ≤ b ≤ c ≤ d ≤ 5 * 10^5)\) probil bilan ajratilgan holda beriladi.
Chiqish faylida bo'lishi mumkin bo'lgan uchburchaklar sonini chop eting.
- 1-test: (1,2,2) (2,2,2) (2,2,3) - 3 ta uchburchak yasash mumkin.
- 2-test: faqat 1 ta teng tomonli uchburchak yasash mumkin.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 2 2 5 |
3 |
| 2 |
300 300 300 300 |
1 |
E. Xilma xil konfetlar 🍬
Xotira: 16 MB, Vaqt: 1000 msO'tkir xilma-xil konfet yeyishni juda yaxshi ko'radi. Ammo unga konfetlarni hammasini yeyishi mumkin emas. O'tkir ko'pi bilan necha xil konfet yeyishi mumkinligini topishga yordam bering! Bizga \(N\) konfetdan iborat \(arr[]\) massivi berilgan, bu yerda \(N\) juft son va \(arr[i]\) konfet turi. Muammo shundaki, agar ulardan faqat \(N/2\) tasini yeyish mumkin bo'lsa, O'tkir yeyishi mumkin bo'lgan har xil turdagi konfetlarning maksimal sonini topishdir.
Birinchi qatorda \(N\) butun juft son – massiv uzunligi beriladi \((1 ≤ N ≤ 2*10^5)\)
Ikkinchi qatorda sizga \(N\) ta son – massiv elementlari beriladi. Massiv elementlari 1018 dan oshmaydi.
Chiqish faylida yagona butun son O'tkir yeyishi mumkin bo'lgan har xil turdagi konfetlarning maksimal sonini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
8 4 4 5 5 6 6 7 7 |
4 |
| 2 |
4 2 2 3 1 |
2 |
F. Tenglik #1
Xotira: 16 MB, Vaqt: 1000 msOyniso, Akobir va 3 ta do'st 1 - sinf o'quvchilari. Ular alifbe bayrami uchun bosh kiyimlar tikishdi va bu bosh kiyimlarga \(a+b=c\) arifmetik ifodaning bo'laklarini yozib olishdi. Ular bayramda yonma yon turib ushbu arfmetik ifodani hosil qilishi kerak edi, afsuski o'yinqaroq sinfdoshlar ifodani chalkashtirib yuborishdi. 3 o'quvchi bosh kiyimiga sonlarni va 2 o'quvchi bosh kiyimiga '\(+\)' va '\(=\)' belgilari yozilgan. Ifodani tuzish tartibi quyidagicha:
- '\(+\)' belgisi '\(=\)' belgisini chap tomonida joylashadi.
- \(a + b = c\) tenglik to'g'ri bo'lishi shart.
- \(a,b\) va \(c\) manfiy bo'lmagan butun(ortiqcha no'llarsiz) sonlar.
Siz Oyniso va Akobirga ifodani qaytadan terib olishida yordam bering.
Kiritish faylida ketma - ket \(a,b,c\) sonlarni birlashib qolishidan hosil bolgan satr |a| + |b| + |c| ≤ 103 beriladi.
Chiqish faylida bolalarni to'g'ri terib chiqilganda bosh kiyimlardagi yozuvlar birlashmasi bolgan ifodani chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
099 |
0+9=9 |
| 2 |
199100 |
1+99=100 |
G. Fibonacci Total
Xotira: 16 MB, Vaqt: 1000 msFibonacci ketma ketligi:
- \(F_1 = 1\),
- \(F_2 = 2\),
- \(F_i = F_i -_1 + F_i -_2, i > 2\).
Shu ketma-ketlik asosida fibonacci hadlarini ko'rib chiqing va \(S = \{s_1, s_2, ..., s_k\}\) ushbu to'plam elementlari yigindisini toping.
- \(\displaystyle\sum_{I=1}^{K} S_i=n\)
Sizning vazifangiz \(n\) soni uchun fibonacci sonlaridan iborat bo'lgan nechata ketma-ketlik tuzish mumkin ekanligini topishdan iborat.
Kiritish faylida Birinchi qatorda testlar soni \(t(1 ≤ t ≤ 10^5)\)
Har bir test uchub alohida qatorlarda \(n (1 ≤ n ≤ 10^{18})\) butun soni kiritiladi.
Agar siz C++ da bolsangiz, Raqamlarni o'qish yoki yozish uchun %lld spesifikatsiyasidan foydalaning. Tavsiya etilgan oqimlar cin, cout yoki %I64d spetsifikatsiyasi.
Chiqish faylida alohida qatorlarda har bir test uchun javobni chiqaring.
1-test:
- n = 13 uchun, S = {13, 5 + 8, 2 + 3 + 8} ketma-ketlik tuzish mumkin.
- n = 16 uchun, S = {3 + 13, 1 + 2 + 13, 3 + 5 + 8, 1 + 2 + 5 + 8} ketma-ketlik tuzish mumkin.
Eslatma:
Agar to'plamda boshqa tuzilgan toplamdagi sonlardan 1 ta bolsa ham farqli son bolsa bu to'plam boshqalaridan farqlanadi. Faqat toplamlardagi sonlarni o'rni almashib kelsa ham ular 1 ta deb hisoblanadi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 13 16 |
3 4 |
H. Aylanadagi qotillar
Xotira: 16 MB, Vaqt: 1000 msAylanada qatl qilinishini kutayotgan n kishi bor. Hisoblash aylananing qaysidir nuqtasidan boshlanadi va aylana bo‘ylab belgilangan yo‘nalishda davom etadi. Har bir qadamda maʼlum miqdordagi odamlar o‘tkazib yuboriladi va keyingi shaxs qatl qilinadi. Yo‘q qilish aylana bo‘ylab davom etadi (qatl qilingan odamlar olib tashlangan sayin kichrayib boraveradi), faqat oxirgi odam qolmaguncha, unga erkinlik beriladi.
\(n\) - kishilarning umumiy soni va k soni hisobga olinsa, bu aylanada \(k-1\) kishi o‘tkazib yuborilganligini va \(k\) - odam o‘ldirilganligini ko‘rsatadi. Vazifa, siz oxirgi bo‘lib omon qolgan odamning joyini topishingiz kerak.
Kirish faylida ikkita raqam \(n , k(1 ≤ n,k ≤ 10^6)\) probel bilan ajratilgan holda beriladi.
Chiqish faylining yagona satrida bitta butun son, oxirgi bo'lib omon qolgan odamning joyini chop eting.
1-test:
- \(n = 5\) va \(k = 2\) bo'lsa, u holda xavfsiz holat 3 ga teng. Birinchidan, 2-pozitsiyadagi odam o'ldiriladi, keyin 4-pozitsiyadagi odam o'ldiriladi, keyin 1-pozitsiyadagi odam o'ldiriladi. Nihoyat, 5-pozitsiyadagi odam o'ldiriladi. Shunday qilib, 3-pozitsiyadagi odam omon qoladi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 2 |
3 |
I. Aylana Stol
Xotira: 16 MB, Vaqt: 1000 msOʻrta asrlarda Gʻarbiy va Markaziy Yevropa mamlakatlarida imtiyozli ijtimoiy qatlam: keng maʼnoda — barcha oqsuyak mulkdorlar (feodallar), tor maʼnoda — faqat mayda oqsuyak mulkdorlar bo'lgan Ritsarlar har oyning biror kunida Dunyoga mashhur "Aylana Stol" o'yinini o'ynashar ekan. Bu o'yin qoidasiga ko'ra Ritsarlar aylana stol atrofida o'tirishadi va har bir Ritsar o'zining raqamiga ega bo'ladi. O'yin sharti shundan iboratki Aylanada o'tirgan odamlardan 1 - raqamlisi Soat strelkasi yo'nalishi bo'yicha o'yini boshlab beradi va yonidagi odamdan keyingisini o'yindan chiqarib yuboradi , shu tarzda o'yin davom etadi, Aylana Stolda oxirgi qolgan 2 Ritsar g'olib bo'ladi.
Kirish faylida n Ritsarlar soni \(n(2 ≤ n ≤ 10^6)\) beriladi.
Chiqish faylida probel bilan ajratilgan holda g'olib bo'lgan 2 Ritsarni raqamini chop eting, yechim mavjud bo'lmasa -1 chop eting.
1 testda :
- n = 5 bo'lsa, qolgan oxirgi 2 Ritsarlarning joylari 1 va 4 ga teng.
- Dastlab: 1 2 3 4 5 => 1 - Ritsar 3 ni chiqaradi,
- Qolganlar : 1 2 4 5 => 2 - Ritsar 5 ni chiqaradi,
- Qolganlar : 1 2 4 => 4 - Ritsar 2 ni chiqaradi.
Natija : 1 4
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 |
1 4 |
| 2 |
10 |
6 10 |
J. Massivdagi Uchlik
Xotira: 16 MB, Vaqt: 1000 msUzunligi \(N\) bo'lgan massiv va \(K\) soni berilgan. Yig‘indisi K ga teng bo‘lgan massivda uchlik bor yoki yo‘qligini toping. Agar massivda shunday uchlik bo'lsa, bu uchlikni chop eting va \(BOR\) deb qaytaring. Aks holda, \(YOQ\) so'zini qaytaring.
Birinchi qatorda \(N\) butun son – massiv uzunligi beriladi \((1 ≤ N ≤ 3000)\)
Ikkinchi qatorda sizga \(N\) ta son – massiv elementlari beriladi. Massiv elementlari\((1 ≤ N ≤ 10^9)\)dan oshmaydi.
Uchinchi qatorda topilishi kerak bo'lgan massivning \(3\) ta elementi yig'indisi \(K\) \((1 ≤ K ≤ 10^{18})\) beriladi.
Chiqish faylining birinchi qatorida \(BOR\) yoki \(YOQ\) so'zi va agar bor bo'lsa keyingi qatorda shu \(3\) ta sonni ketma ket chop eting.
Misol uchun, agar \(N = 5\) va \({ 12, 3, 4, 1, 6, 9 }\) massivi va \(K = 24\) berilgan bo'lsa :
\(12 + 3 + 9 = 24\)
Javob : BOR 12 3 9
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 12 3 4 1 6 9 24 |
BOR 12 3 9 |
| 2 |
4 8 9 5 1 23 |
YOQ |