A. Uchburchak balandligi

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Sof matematik va amaliy xarakterdagi(ayniqsa qurilishda) har xil turdagi muammolarni hal qilishda maʼlum bir geometrik figuraning balandligi qiymatini aniqlash kerak bo‘ladi. Uchburchakda berilgan qiymatni(balandlikni) topish esa juda ham muhim ish . Sizga uchburchak tomonlari beriladi, vazifangiz shu uchburchakni eng kichik balandligini topish.

Kiruvchi ma'lumotlar:

Kiritish faylida \(a, b, c(a, b, c \leqslant 1000)\)butun sonlar probil bilan ajratilgan holda kiritiladi.

Chiquvchi ma'lumotlar:

Chiqish faylida masala yechimini chiqaring. Sizning yechimingiz va javob orasidagi nisbiy hatolik \(10^9\)dan oshmasin.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1 1 1	0.8660254

B. Balandlik

Xotira: 16 MB, Vaqt: 1000 ms

Masala

O’ZBEKISTON TEMIR YO’LLARI AKSIYADORLIK JAMIYATI Yangi temir yo‘l qurilishida muammolar paydo bo‘ldi. Yo'l tepalikli yerlardan o'tadi, ammo yo'llarning o'zi qat'iy gorizontal bo'lishi kerak. Shu sababli, qurilish kompaniyasi rahbariyati ushbu hudud yerlar yuzasini tekislashga qaror qildi. Asosiy muammo shundaki, qurilish maydonchasiga Tuproq olib kirish yoki olib chiqish uchun har bir kubometr uchun 100 ming dollar ketadi. Temir yo'lning byudjeti kichik bo'lgani uchun buni to'lab bilmaydi.

Shuning uchun bosh muhandis faqat tepaliklarni tashkil etuvchi tuproqdan foydalanib, sirtni tekislashga qaror qildi. Vazifa yo'lning dengiz sathidan balandligini aniqlash(har 1 m yer balandligi beriladi). Bu mas'uliyatli vazifa sizga ishonib topshirilgan.

Kiruvchi ma'lumotlar:

INPUT.TXT kirish faylining 1-qatorida balandlik o'lchangan nuqtalarningn soni \(n (1 < n ≤ 30000)\) beriladi. 2-qatorda \(n\) ta manfiy bo'lmagan butun son - har bir o'lchangan tepalikning balandligi \(h_i \space (0 < h_i \le 10000)\) probel bilan ajratilgan holda beriladi.

Chiquvchi ma'lumotlar:

OUTPUT.TXT chiqish fayliga masala javobini \(10^{-10}\) aniqlikda chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	5 2 2 2 2 2	2.0000000000

C. Kvadrat

Xotira: 10 MB, Vaqt: 300 ms

Masala

Dekart koordinatalar tizimida 4 ta d₁, d₂, d₃, d₄ (d_i = (x,y)) nuqta beriladi.

Bu nuqtalardan kordinata o'qlariga paralel bolgan to'g'ri tortburchak bolishi kafolatlanadi. Siz istalgan d_i= (x, y) nuqtani (x,y+1), (x,y−1), (x+1,y) va (x−1,y) nuqtalardan biriga siljitishingiz mumkin boladi. Vazifangiz OX va OY oqlariga paralel bo'lgan kvadrat hosil qilish uchun minimum urinishlarda sonini topishdan iborat.

Berilgan nuqtalar 1 bir xil bo'lmasligi taminlanadi.

Kiruvchi ma'lumotlar:

INPUT.TXT Kiritish faylida 1-qatorda bitta butun son t (1 ≤ t ≤ 10⁴) - test soni.

har bir test uchun 4ta (d_i = (x,y)) nuqta kordinatalari kiritiladi.Har bir satrda ikkita butun son x va y (0 ≤ x,y ≤ 10⁹).

Chiquvchi ma'lumotlar:

OUTPUT.TXT Chiqish faylida Kvadrat olish uchun zarur bo'lgan minimal qadamlar sonini har bir test uchun alohida qatorlarda chop eting.

Izoh:

1-test uchun minimal urinishlar soni quydagicha bo'lishi mumkin:

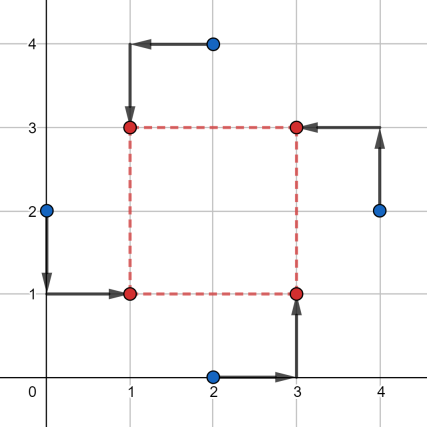
Har bir nuqta ikki marta siljiydi, shuning uchun natija 2+2+2+2=8.
Ikkinchi to'plamda optimal javoblardan biri quyida tasvirlangan:

Natija : 3+1+0+3=7.
Uchinchi to'plamda optimal yurishlardan biri quyida tasvirlangan:

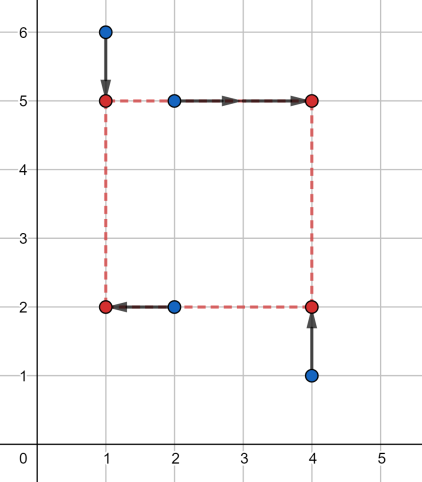
Natija : 1+1+2+1=5.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 0 2 4 2 2 0 2 4 1 0 2 0 4 0 6 0 1 6 2 2 2 5 4 1	8 7 5

D. Shaxmat doskasi

Xotira: 16 MB, Vaqt: 1000 ms

Masala

2 o'yinchi 15 x 15 Shaxmat taxtasida o'yin o'ynashni boshlashdi. O'yin shartlari quydagicha:

O'yin (x,y) kordinatadan boshlanadi. Yuqori chap katakning koordinatalari (1,1), va pastki o'ng katakchada (15,15).
Har bir harakatda o'yinchi Shaxmat toshini quyidagi joylardan biriga ko'chirishi kerak:
1. (x - 2,y + 1)
2. (x - 2,y - 1)
3. (x + 1,y - 2)
4. (x - 1,y - 2)
1-o'yinchidan boshlab, o'yinchilar navbatma-navbat almashadilar. Harakat qila olmagan birinchi o'yinchi o'yinni yo'qotadi(yutqazadi).

Eslatma: Tosh Shaxmat taxtasining chegaralari ichida qolishi kerak.

Quydagi rasmda 8 x 8 Shaxmat taxtasida toshning yura olish yo'llari ko'rsatilgan.

Kiruvchi ma'lumotlar:

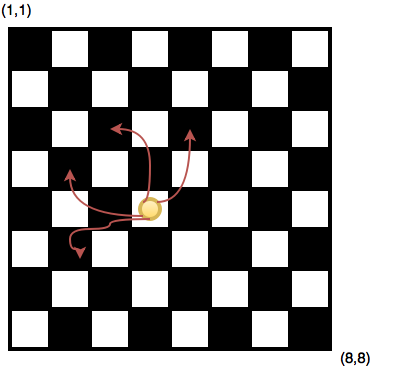
INPUT.TXT Kiritish faylida 1- qatorda t(1 ≤ t ≤ 255) butun son kiritiladi.

Keyingi t ta qatorda (x,y)(1 ≤ x_i, y_i ≤ 15) kiritiladi.

Chiquvchi ma'lumotlar:

OUTPUT.TXT Chiqish faylida har bir test uchun alohida qatorlarda O'yinchilardan 1 - si golib bo'lsa " bir" aks holda "ikki" deb chiqaring.

Izoh:

Birinchi holda, o'yinchi1 qizil kvadratdan boshlanadi va ko'k kvadratlarning istalganiga o'tishi mumkin. Qaysi biri tanlanganidan qat'iy nazar, o'yinchi2 o'yinda g'alaba qozonish uchun yashil kvadratlardan biriga o'tishi mumkin.

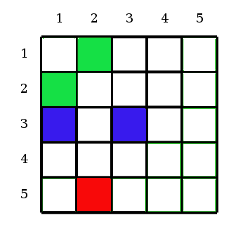
Ikkinchi holda, 1-o'yinchi qizil kvadratdan boshlanadi va har qanday ko'k yoki binafsha kvadratga o'tishi mumkin. Binafsha rangga o'tish 2-o'yinchini sariq kvadrat bilan cheklaydi. Sariq kvadratdan 1-o'yinchi yashil maydonga o'tadi va g'alaba qozonadi.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 5 2 5 3 8 8	ikki bir bir

E. Max Sum Modul

Xotira: 16 MB, Vaqt: 1000 ms

Masala

n ta butun sondan iborat bo'lgan sonli ketma ketlik berilgan. Shu ketma ketlik ichidan shunday ketma ketlik olinki modul jihatidan bu sonlar yigindisi eng katta bo'lsin.

Eslatma: |x| - x ≥ 0 bo'lsa x , x < 0 bo'lsa x ga tengdir.

Kiruvchi ma'lumotlar:

INPUT.TXT Kiritish faylida 1-qatorda n (1 ≤ n ≤ 10000) butun son beriladi. 2-qatorda n ta son(\(-10^6\) ≤ a_i ≤ 10⁶) probil bilan ajratilgan holda beriladi.

Chiquvchi ma'lumotlar:

OUTPUT.TXT Chiqish faylida 1 - qatorida siz tanlagan ketma-ketlikning k uzunligini chop eting. 2 - qatorda probil bilan k ta sonli ketma ketlikni elementlari joylashuvdagi o'rinlarini chop eting.

Izoh:

1-test:

Misollar:

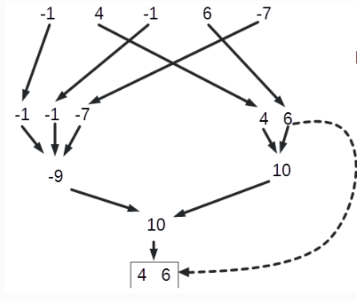
#	INPUT.TXT	OUTPUT.TXT
1	5 -1 4 -1 6 -7	2 2 4

F. Queue Game

Xotira: 10 MB, Vaqt: 300 ms

Masala

2 ta do'st, Akobir va Quvonchbek "Queue" game o'yini o'ynashmoqda. Bu o'yin shartiga ko'ra o'yinchilarga \(n\) ta sondan iborat sonlar to'plami \((a_1, a_2, a_3, ..., a_n)\) beriladi, o'yinni Akobir boshlab beradi. Akobir eng katta soni olib tashlaydi, Quvonchbek esa eng kichigini, shu tariqa o'yin davom etadi. Oxirida qolgan o'yinchi g'olib boladi. Sizning vazifangiz oxirida go'lib bo'lgan o'yinchi necha soni bilan qolganini topishdan iborat.

Kiruvchi ma'lumotlar:

Kiritish faylida 1-qatorida \(n (1 ≤ n ≤ 1000)\) butun soni kiritiladi. 2-qatorida \(n\) ta butun sonlar toplami \((a_1,a_2,…,a_n)(1 ≤ a_i ≤ 10^6)\) kiritiladi.

Chiquvchi ma'lumotlar:

Chiqish faylida g'olib bo'lgan o'yinchiga qolgan raqamni chop eting.

Izoh:

1-test:

Akobir sonlarda 3 ni olib tashlaydi.
Quvonchbek 1 ni olib tashlaydi.
Akobir g'olib.

Natija: 2.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 2 1 3	2

G. Max Son

Xotira: 64 MB, Vaqt: 1000 ms

Masala

Sizga \(a, b\) sonlari beriladi, \([a, b]\) oraliqda raqamlari yig'indisi eng katta bo'ladigan tub sonni topishingiz kerak.

Kiruvchi ma'lumotlar:

Kiritish faylida \(a\) va \(b\) \((1 ≤ a ≤ b ≤ 10^8)\) butun sonlar beriladi.

Chiquvchi ma'lumotlar:

Chiqish faylida masala javobini chop eting. Agar bunday sonlar bir nechta bolsa eng kattasini chiqaring. \([a,b]\) oraliqda tub son mavjud bo'lmasa -1 ni chiqaring

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1 13	7
2	900 1000	997
3	8 10	-1