A. O’chirish #1
Xotira: 16 MB, Vaqt: 1000 msUzunligi \(2n\) bo’lgan \(a\) massiv berilgan. Massiv elementlari \([1..n]\) oralig’ida bo’lib, har bir qiymat massivda aniq 2 martadan uchraydi(ya’ni 1 ikki marta, 2 ikki marta, ..., n ikki marta). Massiv ustida quyidagi ikki amallarni bajarish mumkin:
- Massivning ikki qo’shni elementini (\(a[i]\) va \(a[i + 1] (1 ≤ i < n)\)) o’rnini almashtirish
- Massivdagi ikkita bir xil qiymatli qo’shni elementlarni o’chirib tashlash. Masalan \([1, 2, 2, 3, 1, 3]\) massivdan ikkita yonma-yon 2 lar o’chirib tashlanganindan so’ng massiv \([1, 3, 1, 3]\) ko’rinishga keladi.
Yuqoridagi amallarni ixtiyoriy tartibda bajarish mumkin bo’lsa, massivdagi barcha elementlarni o’chirib tashlash uchun kerak bo’ladigan minimal amallar sonini chiqaring.
Birinchi qatorda bitta butun son \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Keyingi qatorda \(2n\) ta butun son - massiv elementlari \(a_1, a_2, ..., a_n\) kiritiladi \((1 ≤ a_i ≤ n)\).
1-subtask (7 ball): Bir xil qiymatli sonlar massivda yonma-yon joylashgan \((1 ≤ n ≤ 10^5)\).
2-subtask (8 ball): Bir xil qiymatli sonlar o’rtasida ko’pi bilan bitta boshqa son bor \((1 ≤ n ≤ 100)\).
3-subtask (11 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 1000)\).
4-subtask (16 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 10^5)\).
5-subtask (22 ball): \(1 ≤ n ≤ 1000\)
6-subtask (36 ball): \(1 ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda, quyidagicha 4 ta amal bajarish mumkin:
1) 3- va 4- o’rindagi elementlarni o’rnini almashtiramiz, massiv [3, 1, 1, 2, 2, 3] ko’rinishda.
2) 1 qiymatli elementlarni o’chirib tashlaymiz - [3, 2, 2, 3]
3) 2 qiymatli elementlarni o’chirib tashlaymiz - [3, 3]
4) Vanihoyat, 3 qiymatli elementlarni o’chirib tashlaymiz - []
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 1 2 1 2 3 |
4 |
B. O’chirish #2
Xotira: 16 MB, Vaqt: 1000 msUzunligi \(2n\) bo’lgan \(a\) massiv berilgan. Massiv elementlari \([1..n]\) oralig’ida bo’lib, har bir qiymat massivda aniq 2 martadan uchraydi(ya’ni 1 ikki marta, 2 ikki marta, ..., n ikki marta). Massiv ustida quyidagi ikki amallarni bajarish mumkin:
- Massivning ikki qo’shni elementini (\(a[i]\) va \(a[i + 1] (1 ≤ i < n)\)) o’rnini almashtirish
- Massivdagi ikkita bir xil qiymatli qo’shni elementlarni o’chirib tashlash. Masalan \([1, 2, 2, 3, 1, 3]\) massivdan ikkita yonma-yon 2 lar o’chirib tashlanganindan so’ng massiv \([1, 3, 1, 3]\) ko’rinishga keladi.
Yuqoridagi amallarni ixtiyoriy tartibda bajarish mumkin bo’lsa, massivdagi barcha elementlarni o’chirib tashlash uchun kerak bo’ladigan minimal amallar sonini chiqaring.
Birinchi qatorda bitta butun son \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Keyingi qatorda \(2n\) ta butun son - massiv elementlari \(a_1, a_2, ..., a_n\) kiritiladi \((1 ≤ a_i ≤ n)\).
1-subtask (7 ball): Bir xil qiymatli sonlar massivda yonma-yon joylashgan \((1 ≤ n ≤ 10^5)\).
2-subtask (8 ball): Bir xil qiymatli sonlar o’rtasida ko’pi bilan bitta boshqa son bor \((1 ≤ n ≤ 100)\).
3-subtask (11 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 1000)\).
4-subtask (16 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 10^5)\).
5-subtask (22 ball): \(1 ≤ n ≤ 1000\)
6-subtask (36 ball): \(1 ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda, quyidagicha 4 ta amal bajarish mumkin:
1) 3- va 4- o’rindagi elementlarni o’rnini almashtiramiz, massiv [3, 1, 1, 2, 2, 3] ko’rinishda.
2) 1 qiymatli elementlarni o’chirib tashlaymiz - [3, 2, 2, 3]
3) 2 qiymatli elementlarni o’chirib tashlaymiz - [3, 3]
4) Vanihoyat, 3 qiymatli elementlarni o’chirib tashlaymiz - []
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 1 2 1 2 3 |
4 |
C. O’chirish #3
Xotira: 16 MB, Vaqt: 1000 msUzunligi \(2n\) bo’lgan \(a\) massiv berilgan. Massiv elementlari \([1..n]\) oralig’ida bo’lib, har bir qiymat massivda aniq 2 martadan uchraydi(ya’ni 1 ikki marta, 2 ikki marta, ..., n ikki marta). Massiv ustida quyidagi ikki amallarni bajarish mumkin:
- Massivning ikki qo’shni elementini (\(a[i]\) va \(a[i + 1] (1 ≤ i < n)\)) o’rnini almashtirish
- Massivdagi ikkita bir xil qiymatli qo’shni elementlarni o’chirib tashlash. Masalan \([1, 2, 2, 3, 1, 3]\) massivdan ikkita yonma-yon 2 lar o’chirib tashlanganindan so’ng massiv \([1, 3, 1, 3]\) ko’rinishga keladi.
Yuqoridagi amallarni ixtiyoriy tartibda bajarish mumkin bo’lsa, massivdagi barcha elementlarni o’chirib tashlash uchun kerak bo’ladigan minimal amallar sonini chiqaring.
Birinchi qatorda bitta butun son \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Keyingi qatorda \(2n\) ta butun son - massiv elementlari \(a_1, a_2, ..., a_n\) kiritiladi \((1 ≤ a_i ≤ n)\).
1-subtask (7 ball): Bir xil qiymatli sonlar massivda yonma-yon joylashgan \((1 ≤ n ≤ 10^5)\).
2-subtask (8 ball): Bir xil qiymatli sonlar o’rtasida ko’pi bilan bitta boshqa son bor \((1 ≤ n ≤ 100)\).
3-subtask (11 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 1000)\).
4-subtask (16 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 10^5)\).
5-subtask (22 ball): \(1 ≤ n ≤ 1000\)
6-subtask (36 ball): \(1 ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda, quyidagicha 4 ta amal bajarish mumkin:
1) 3- va 4- o’rindagi elementlarni o’rnini almashtiramiz, massiv [3, 1, 1, 2, 2, 3] ko’rinishda.
2) 1 qiymatli elementlarni o’chirib tashlaymiz - [3, 2, 2, 3]
3) 2 qiymatli elementlarni o’chirib tashlaymiz - [3, 3]
4) Vanihoyat, 3 qiymatli elementlarni o’chirib tashlaymiz - []
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 1 2 1 2 3 |
4 |
D. O’chirish #4
Xotira: 16 MB, Vaqt: 1000 msUzunligi \(2n\) bo’lgan \(a\) massiv berilgan. Massiv elementlari \([1..n]\) oralig’ida bo’lib, har bir qiymat massivda aniq 2 martadan uchraydi(ya’ni 1 ikki marta, 2 ikki marta, ..., n ikki marta). Massiv ustida quyidagi ikki amallarni bajarish mumkin:
- Massivning ikki qo’shni elementini (\(a[i]\) va \(a[i + 1] (1 ≤ i < n)\)) o’rnini almashtirish
- Massivdagi ikkita bir xil qiymatli qo’shni elementlarni o’chirib tashlash. Masalan \([1, 2, 2, 3, 1, 3]\) massivdan ikkita yonma-yon 2 lar o’chirib tashlanganindan so’ng massiv \([1, 3, 1, 3]\) ko’rinishga keladi.
Yuqoridagi amallarni ixtiyoriy tartibda bajarish mumkin bo’lsa, massivdagi barcha elementlarni o’chirib tashlash uchun kerak bo’ladigan minimal amallar sonini chiqaring.
Birinchi qatorda bitta butun son \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Keyingi qatorda \(2n\) ta butun son - massiv elementlari \(a_1, a_2, ..., a_n\) kiritiladi \((1 ≤ a_i ≤ n)\).
1-subtask (7 ball): Bir xil qiymatli sonlar massivda yonma-yon joylashgan \((1 ≤ n ≤ 10^5)\).
2-subtask (8 ball): Bir xil qiymatli sonlar o’rtasida ko’pi bilan bitta boshqa son bor \((1 ≤ n ≤ 100)\).
3-subtask (11 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 1000)\).
4-subtask (16 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 10^5)\).
5-subtask (22 ball): \(1 ≤ n ≤ 1000\)
6-subtask (36 ball): \(1 ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda, quyidagicha 4 ta amal bajarish mumkin:
1) 3- va 4- o’rindagi elementlarni o’rnini almashtiramiz, massiv [3, 1, 1, 2, 2, 3] ko’rinishda.
2) 1 qiymatli elementlarni o’chirib tashlaymiz - [3, 2, 2, 3]
3) 2 qiymatli elementlarni o’chirib tashlaymiz - [3, 3]
4) Vanihoyat, 3 qiymatli elementlarni o’chirib tashlaymiz - []
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 1 2 1 2 3 |
4 |
E. O’chirish #5
Xotira: 16 MB, Vaqt: 1000 msUzunligi \(2n\) bo’lgan \(a\) massiv berilgan. Massiv elementlari \([1..n]\) oralig’ida bo’lib, har bir qiymat massivda aniq 2 martadan uchraydi(ya’ni 1 ikki marta, 2 ikki marta, ..., n ikki marta). Massiv ustida quyidagi ikki amallarni bajarish mumkin:
- Massivning ikki qo’shni elementini (\(a[i]\) va \(a[i + 1] (1 ≤ i < n)\)) o’rnini almashtirish
- Massivdagi ikkita bir xil qiymatli qo’shni elementlarni o’chirib tashlash. Masalan \([1, 2, 2, 3, 1, 3]\) massivdan ikkita yonma-yon 2 lar o’chirib tashlanganindan so’ng massiv \([1, 3, 1, 3]\) ko’rinishga keladi.
Yuqoridagi amallarni ixtiyoriy tartibda bajarish mumkin bo’lsa, massivdagi barcha elementlarni o’chirib tashlash uchun kerak bo’ladigan minimal amallar sonini chiqaring.
Birinchi qatorda bitta butun son \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Keyingi qatorda \(2n\) ta butun son - massiv elementlari \(a_1, a_2, ..., a_n\) kiritiladi \((1 ≤ a_i ≤ n)\).
1-subtask (7 ball): Bir xil qiymatli sonlar massivda yonma-yon joylashgan \((1 ≤ n ≤ 10^5)\).
2-subtask (8 ball): Bir xil qiymatli sonlar o’rtasida ko’pi bilan bitta boshqa son bor \((1 ≤ n ≤ 100)\).
3-subtask (11 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 1000)\).
4-subtask (16 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 10^5)\).
5-subtask (22 ball): \(1 ≤ n ≤ 1000\)
6-subtask (36 ball): \(1 ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda, quyidagicha 4 ta amal bajarish mumkin:
1) 3- va 4- o’rindagi elementlarni o’rnini almashtiramiz, massiv [3, 1, 1, 2, 2, 3] ko’rinishda.
2) 1 qiymatli elementlarni o’chirib tashlaymiz - [3, 2, 2, 3]
3) 2 qiymatli elementlarni o’chirib tashlaymiz - [3, 3]
4) Vanihoyat, 3 qiymatli elementlarni o’chirib tashlaymiz - []
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 1 2 1 2 3 |
4 |
F. O’chirish #6
Xotira: 16 MB, Vaqt: 1000 msUzunligi \(2n\) bo’lgan \(a\) massiv berilgan. Massiv elementlari \([1..n]\) oralig’ida bo’lib, har bir qiymat massivda aniq 2 martadan uchraydi(ya’ni 1 ikki marta, 2 ikki marta, ..., n ikki marta). Massiv ustida quyidagi ikki amallarni bajarish mumkin:
- Massivning ikki qo’shni elementini (\(a[i]\) va \(a[i + 1] (1 ≤ i < n)\)) o’rnini almashtirish
- Massivdagi ikkita bir xil qiymatli qo’shni elementlarni o’chirib tashlash. Masalan \([1, 2, 2, 3, 1, 3]\) massivdan ikkita yonma-yon 2 lar o’chirib tashlanganindan so’ng massiv \([1, 3, 1, 3]\) ko’rinishga keladi.
Yuqoridagi amallarni ixtiyoriy tartibda bajarish mumkin bo’lsa, massivdagi barcha elementlarni o’chirib tashlash uchun kerak bo’ladigan minimal amallar sonini chiqaring.
Birinchi qatorda bitta butun son \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Keyingi qatorda \(2n\) ta butun son - massiv elementlari \(a_1, a_2, ..., a_n\) kiritiladi \((1 ≤ a_i ≤ n)\).
1-subtask (7 ball): Bir xil qiymatli sonlar massivda yonma-yon joylashgan \((1 ≤ n ≤ 10^5)\).
2-subtask (8 ball): Bir xil qiymatli sonlar o’rtasida ko’pi bilan bitta boshqa son bor \((1 ≤ n ≤ 100)\).
3-subtask (11 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 1000)\).
4-subtask (16 ball): Massivning dastlabki \(n\) ta elementi \(1, 2, 3,...,n\) sonlardan iborat, ammo sonlar o’rni ixtiyoriy bo’lishi mumkin \((1 ≤ n ≤ 10^5)\).
5-subtask (22 ball): \(1 ≤ n ≤ 1000\)
6-subtask (36 ball): \(1 ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda, quyidagicha 4 ta amal bajarish mumkin:
1) 3- va 4- o’rindagi elementlarni o’rnini almashtiramiz, massiv [3, 1, 1, 2, 2, 3] ko’rinishda.
2) 1 qiymatli elementlarni o’chirib tashlaymiz - [3, 2, 2, 3]
3) 2 qiymatli elementlarni o’chirib tashlaymiz - [3, 3]
4) Vanihoyat, 3 qiymatli elementlarni o’chirib tashlaymiz - []
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 1 2 1 2 3 |
4 |
G. Gilos #1
Xotira: 16 MB, Vaqt: 1000 msIkki do’st Hoshimjon va Orif ta’tilning keyingi n kuni davomida gilos terishmoqchi. Ammo do’stlar har doim ham o’zlari xohlaganchalik giloslarni tera olishmaydi va shunga qarab ularning kayfiyati o’zgarishi mumkin. Boshqacha qilib aytkanda do’stlar \(i\)-kuni gilos tersa Hoshimjonni kayfiyatiga \(a_i\), Orifnikiga esa \(b_i\) qo’shiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Sizga \(l\) va \(r\) ko’rinishidagi \(q\) ta so’rov beriladi. Agar do’stlar \([l..r]\) oralig’idagi kunlarning har birida gilos teradigan bo’lsa, shu oraliqdagi do’stlarning umumiy xursandchilik koeffitsientini toping. Umumiy xursandchilik koeffitsienti quyidagicha hisoblanadi:
- Dastlab, \(l\)-kundan oldin, har bir bolaning kayfiyati 0 ga teng bo’ladi
- \(i\) - kuni \((l ≤ i ≤ r)\) Hoshimjonning kayfiyati \(a_i\) ga, Orifni kayfiyati \(b_i\) ga o’zgaradi
- \(i\) - kun \((l ≤ i ≤ r)\) uchun do’stlarning xursandchilik koeffitsienti Hoshimjon va Orifni shu kundagi kayfiyatlarini kattasiga teng bo’ladi
- umumiy xursandchilik koeffitsienti barcha \(r - l + 1\) kunlardagi xursandchilik koeffitsientlari yig’indisiga teng.
To’liqroq tushunish uchun quyida keltirilgan misolga qarang.
Birinchi qatorda kunlar soni \(n\) va so’rovlar soni \(q\) kiritiladi \((1 ≤ n, q ≤ 10^5)\). Ikkinchi qatorda \(n\) ta butun son \(a_1, a_2, ..., a_n\) va 3-qatorda ham \(n\) ta butun son \(b_1, b_2, ..., b_n\) kiritiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Keyingi \(q\) ta qatorda so’rovlar \(l\) va \(r\) butun sonlari ko’rinishida beriladi \((1 ≤ l ≤ r ≤ n)\).
1-subtask(9 ball): \(n, q ≤ 1000\).
2-subtask(7 ball): \(a_i = 1, b_i = 0, n, q ≤ 10^5\)
3-subtask(13 ball): \(a_i ≥ 0, b_i = 0, n, q ≤ 10^5\)
4-subtask(29 ball): \(b_i = 0, n, q ≤ 10^5\)
5-subtask(42 ball): \(n, q ≤ 10^5\)
Har bir so’rov uchun umumiy xursandchilik koeffitsientini chiqaring.
Birinchi misoldagi uchinchi so’rovni ko’raylik, do’stlar 2..4 kunlar oralig’ida gilos terishadi.
Dastlab, Hoshimjonning ham Orifning ham kayfiyati 0 ga teng.
2-kundan so’ng: Hoshimjonni kayfiyati = -5, Orifni kayfiyati = 20, xursandlik koeffitsienti 20 (chunki 20 > -5).
3-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 = 3, Orifni kayfiyati = 20 + 9 = 29, xursandlik koeffitsienti 29 (chunki 29 > 3).
4-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 + (-10) = -7, Orifni kayfiyati = 20 + 9 + (-100) = -71, xursandlik koeffitsienti -7 (chunki -7 > -100).
Shunday qilib, umumiy xursandlik koeffitsienti = 20 + 29 + (-7) = 42.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 7 3 -5 8 -10 3 7 -4 20 9 -100 105 20 1 6 1 5 2 4 3 3 3 6 2 5 4 5 |
120 70 42 9 55 76 -5 |
H. Gilos #2
Xotira: 16 MB, Vaqt: 1000 msIkki do’st Hoshimjon va Orif ta’tilning keyingi n kuni davomida gilos terishmoqchi. Ammo do’stlar har doim ham o’zlari xohlaganchalik giloslarni tera olishmaydi va shunga qarab ularning kayfiyati o’zgarishi mumkin. Boshqacha qilib aytkanda do’stlar \(i\)-kuni gilos tersa Hoshimjonni kayfiyatiga \(a_i\), Orifnikiga esa \(b_i\) qo’shiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Sizga \(l\) va \(r\) ko’rinishidagi \(q\) ta so’rov beriladi. Agar do’stlar \([l..r]\) oralig’idagi kunlarning har birida gilos teradigan bo’lsa, shu oraliqdagi do’stlarning umumiy xursandchilik koeffitsientini toping. Umumiy xursandchilik koeffitsienti quyidagicha hisoblanadi:
- Dastlab, \(l\)-kundan oldin, har bir bolaning kayfiyati 0 ga teng bo’ladi
- \(i\) - kuni \((l ≤ i ≤ r)\) Hoshimjonning kayfiyati \(a_i\) ga, Orifni kayfiyati \(b_i\) ga o’zgaradi
- \(i\) - kun \((l ≤ i ≤ r)\) uchun do’stlarning xursandchilik koeffitsienti Hoshimjon va Orifni shu kundagi kayfiyatlarini kattasiga teng bo’ladi
- umumiy xursandchilik koeffitsienti barcha \(r - l + 1\) kunlardagi xursandchilik koeffitsientlari yig’indisiga teng.
To’liqroq tushunish uchun quyida keltirilgan misolga qarang.
Birinchi qatorda kunlar soni \(n\) va so’rovlar soni \(q\) kiritiladi \((1 ≤ n, q ≤ 10^5)\). Ikkinchi qatorda \(n\) ta butun son \(a_1, a_2, ..., a_n\) va 3-qatorda ham \(n\) ta butun son \(b_1, b_2, ..., b_n\) kiritiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Keyingi \(q\) ta qatorda so’rovlar \(l\) va \(r\) butun sonlari ko’rinishida beriladi \((1 ≤ l ≤ r ≤ n)\).
1-subtask(9 ball): \(n, q ≤ 1000\).
2-subtask(7 ball): \(a_i = 1, b_i = 0, n, q ≤ 10^5\)
3-subtask(13 ball): \(a_i ≥ 0, b_i = 0, n, q ≤ 10^5\)
4-subtask(29 ball): \(b_i = 0, n, q ≤ 10^5\)
5-subtask(42 ball): \(n, q ≤ 10^5\)
Har bir so’rov uchun umumiy xursandchilik koeffitsientini chiqaring.
Birinchi misoldagi uchinchi so’rovni ko’raylik, do’stlar 2..4 kunlar oralig’ida gilos terishadi.
Dastlab, Hoshimjonning ham Orifning ham kayfiyati 0 ga teng.
2-kundan so’ng: Hoshimjonni kayfiyati = -5, Orifni kayfiyati = 20, xursandlik koeffitsienti 20 (chunki 20 > -5).
3-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 = 3, Orifni kayfiyati = 20 + 9 = 29, xursandlik koeffitsienti 29 (chunki 29 > 3).
4-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 + (-10) = -7, Orifni kayfiyati = 20 + 9 + (-100) = -71, xursandlik koeffitsienti -7 (chunki -7 > -100).
Shunday qilib, umumiy xursandlik koeffitsienti = 20 + 29 + (-7) = 42.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 7 3 -5 8 -10 3 7 -4 20 9 -100 105 20 1 6 1 5 2 4 3 3 3 6 2 5 4 5 |
120 70 42 9 55 76 -5 |
I. Gilos #3
Xotira: 16 MB, Vaqt: 1000 msIkki do’st Hoshimjon va Orif ta’tilning keyingi n kuni davomida gilos terishmoqchi. Ammo do’stlar har doim ham o’zlari xohlaganchalik giloslarni tera olishmaydi va shunga qarab ularning kayfiyati o’zgarishi mumkin. Boshqacha qilib aytkanda do’stlar \(i\)-kuni gilos tersa Hoshimjonni kayfiyatiga \(a_i\), Orifnikiga esa \(b_i\) qo’shiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Sizga \(l\) va \(r\) ko’rinishidagi \(q\) ta so’rov beriladi. Agar do’stlar \([l..r]\) oralig’idagi kunlarning har birida gilos teradigan bo’lsa, shu oraliqdagi do’stlarning umumiy xursandchilik koeffitsientini toping. Umumiy xursandchilik koeffitsienti quyidagicha hisoblanadi:
- Dastlab, \(l\)-kundan oldin, har bir bolaning kayfiyati 0 ga teng bo’ladi
- \(i\) - kuni \((l ≤ i ≤ r)\) Hoshimjonning kayfiyati \(a_i\) ga, Orifni kayfiyati \(b_i\) ga o’zgaradi
- \(i\) - kun \((l ≤ i ≤ r)\) uchun do’stlarning xursandchilik koeffitsienti Hoshimjon va Orifni shu kundagi kayfiyatlarini kattasiga teng bo’ladi
- umumiy xursandchilik koeffitsienti barcha \(r - l + 1\) kunlardagi xursandchilik koeffitsientlari yig’indisiga teng.
To’liqroq tushunish uchun quyida keltirilgan misolga qarang.
Birinchi qatorda kunlar soni \(n\) va so’rovlar soni \(q\) kiritiladi \((1 ≤ n, q ≤ 10^5)\). Ikkinchi qatorda \(n\) ta butun son \(a_1, a_2, ..., a_n\) va 3-qatorda ham \(n\) ta butun son \(b_1, b_2, ..., b_n\) kiritiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Keyingi \(q\) ta qatorda so’rovlar \(l\) va \(r\) butun sonlari ko’rinishida beriladi \((1 ≤ l ≤ r ≤ n)\).
1-subtask(9 ball): \(n, q ≤ 1000\).
2-subtask(7 ball): \(a_i = 1, b_i = 0, n, q ≤ 10^5\)
3-subtask(13 ball): \(a_i ≥ 0, b_i = 0, n, q ≤ 10^5\)
4-subtask(29 ball): \(b_i = 0, n, q ≤ 10^5\)
5-subtask(42 ball): \(n, q ≤ 10^5\)
Har bir so’rov uchun umumiy xursandchilik koeffitsientini chiqaring.
Birinchi misoldagi uchinchi so’rovni ko’raylik, do’stlar 2..4 kunlar oralig’ida gilos terishadi.
Dastlab, Hoshimjonning ham Orifning ham kayfiyati 0 ga teng.
2-kundan so’ng: Hoshimjonni kayfiyati = -5, Orifni kayfiyati = 20, xursandlik koeffitsienti 20 (chunki 20 > -5).
3-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 = 3, Orifni kayfiyati = 20 + 9 = 29, xursandlik koeffitsienti 29 (chunki 29 > 3).
4-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 + (-10) = -7, Orifni kayfiyati = 20 + 9 + (-100) = -71, xursandlik koeffitsienti -7 (chunki -7 > -100).
Shunday qilib, umumiy xursandlik koeffitsienti = 20 + 29 + (-7) = 42.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 7 3 -5 8 -10 3 7 -4 20 9 -100 105 20 1 6 1 5 2 4 3 3 3 6 2 5 4 5 |
120 70 42 9 55 76 -5 |
J. Gilos #4
Xotira: 16 MB, Vaqt: 1000 msIkki do’st Hoshimjon va Orif ta’tilning keyingi n kuni davomida gilos terishmoqchi. Ammo do’stlar har doim ham o’zlari xohlaganchalik giloslarni tera olishmaydi va shunga qarab ularning kayfiyati o’zgarishi mumkin. Boshqacha qilib aytkanda do’stlar \(i\)-kuni gilos tersa Hoshimjonni kayfiyatiga \(a_i\), Orifnikiga esa \(b_i\) qo’shiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Sizga \(l\) va \(r\) ko’rinishidagi \(q\) ta so’rov beriladi. Agar do’stlar \([l..r]\) oralig’idagi kunlarning har birida gilos teradigan bo’lsa, shu oraliqdagi do’stlarning umumiy xursandchilik koeffitsientini toping. Umumiy xursandchilik koeffitsienti quyidagicha hisoblanadi:
- Dastlab, \(l\)-kundan oldin, har bir bolaning kayfiyati 0 ga teng bo’ladi
- \(i\) - kuni \((l ≤ i ≤ r)\) Hoshimjonning kayfiyati \(a_i\) ga, Orifni kayfiyati \(b_i\) ga o’zgaradi
- \(i\) - kun \((l ≤ i ≤ r)\) uchun do’stlarning xursandchilik koeffitsienti Hoshimjon va Orifni shu kundagi kayfiyatlarini kattasiga teng bo’ladi
- umumiy xursandchilik koeffitsienti barcha \(r - l + 1\) kunlardagi xursandchilik koeffitsientlari yig’indisiga teng.
To’liqroq tushunish uchun quyida keltirilgan misolga qarang.
Birinchi qatorda kunlar soni \(n\) va so’rovlar soni \(q\) kiritiladi \((1 ≤ n, q ≤ 10^5)\). Ikkinchi qatorda \(n\) ta butun son \(a_1, a_2, ..., a_n\) va 3-qatorda ham \(n\) ta butun son \(b_1, b_2, ..., b_n\) kiritiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Keyingi \(q\) ta qatorda so’rovlar \(l\) va \(r\) butun sonlari ko’rinishida beriladi \((1 ≤ l ≤ r ≤ n)\).
1-subtask(9 ball): \(n, q ≤ 1000\).
2-subtask(7 ball): \(a_i = 1, b_i = 0, n, q ≤ 10^5\)
3-subtask(13 ball): \(a_i ≥ 0, b_i = 0, n, q ≤ 10^5\)
4-subtask(29 ball): \(b_i = 0, n, q ≤ 10^5\)
5-subtask(42 ball): \(n, q ≤ 10^5\)
Har bir so’rov uchun umumiy xursandchilik koeffitsientini chiqaring.
Birinchi misoldagi uchinchi so’rovni ko’raylik, do’stlar 2..4 kunlar oralig’ida gilos terishadi.
Dastlab, Hoshimjonning ham Orifning ham kayfiyati 0 ga teng.
2-kundan so’ng: Hoshimjonni kayfiyati = -5, Orifni kayfiyati = 20, xursandlik koeffitsienti 20 (chunki 20 > -5).
3-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 = 3, Orifni kayfiyati = 20 + 9 = 29, xursandlik koeffitsienti 29 (chunki 29 > 3).
4-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 + (-10) = -7, Orifni kayfiyati = 20 + 9 + (-100) = -71, xursandlik koeffitsienti -7 (chunki -7 > -100).
Shunday qilib, umumiy xursandlik koeffitsienti = 20 + 29 + (-7) = 42.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 7 3 -5 8 -10 3 7 -4 20 9 -100 105 20 1 6 1 5 2 4 3 3 3 6 2 5 4 5 |
120 70 42 9 55 76 -5 |
K. Gilos #5
Xotira: 64 MB, Vaqt: 1000 msIkki do’st Hoshimjon va Orif ta’tilning keyingi n kuni davomida gilos terishmoqchi. Ammo do’stlar har doim ham o’zlari xohlaganchalik giloslarni tera olishmaydi va shunga qarab ularning kayfiyati o’zgarishi mumkin. Boshqacha qilib aytkanda do’stlar \(i\)-kuni gilos tersa Hoshimjonni kayfiyatiga \(a_i\), Orifnikiga esa \(b_i\) qo’shiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Sizga \(l\) va \(r\) ko’rinishidagi \(q\) ta so’rov beriladi. Agar do’stlar \([l..r]\) oralig’idagi kunlarning har birida gilos teradigan bo’lsa, shu oraliqdagi do’stlarning umumiy xursandchilik koeffitsientini toping. Umumiy xursandchilik koeffitsienti quyidagicha hisoblanadi:
- Dastlab, \(l\)-kundan oldin, har bir bolaning kayfiyati 0 ga teng bo’ladi
- \(i\) - kuni \((l ≤ i ≤ r)\) Hoshimjonning kayfiyati \(a_i\) ga, Orifni kayfiyati \(b_i\) ga o’zgaradi
- \(i\) - kun \((l ≤ i ≤ r)\) uchun do’stlarning xursandchilik koeffitsienti Hoshimjon va Orifni shu kundagi kayfiyatlarini kattasiga teng bo’ladi
- umumiy xursandchilik koeffitsienti barcha \(r - l + 1\) kunlardagi xursandchilik koeffitsientlari yig’indisiga teng.
To’liqroq tushunish uchun quyida keltirilgan misolga qarang.
Birinchi qatorda kunlar soni \(n\) va so’rovlar soni \(q\) kiritiladi \((1 ≤ n, q ≤ 10^5)\). Ikkinchi qatorda \(n\) ta butun son \(a_1, a_2, ..., a_n\) va 3-qatorda ham \(n\) ta butun son \(b_1, b_2, ..., b_n\) kiritiladi \((-10^6 ≤ a_i, b_i ≤ 10^6)\).
Keyingi \(q\) ta qatorda so’rovlar \(l\) va \(r\) butun sonlari ko’rinishida beriladi \((1 ≤ l ≤ r ≤ n)\).
1-subtask(9 ball): \(n, q ≤ 1000\).
2-subtask(7 ball): \(a_i = 1, b_i = 0, n, q ≤ 10^5\)
3-subtask(13 ball): \(a_i ≥ 0, b_i = 0, n, q ≤ 10^5\)
4-subtask(29 ball): \(b_i = 0, n, q ≤ 10^5\)
5-subtask(42 ball): \(n, q ≤ 10^5\)
Har bir so’rov uchun umumiy xursandchilik koeffitsientini chiqaring.
Birinchi misoldagi uchinchi so’rovni ko’raylik, do’stlar 2..4 kunlar oralig’ida gilos terishadi.
Dastlab, Hoshimjonning ham Orifning ham kayfiyati 0 ga teng.
2-kundan so’ng: Hoshimjonni kayfiyati = -5, Orifni kayfiyati = 20, xursandlik koeffitsienti 20 (chunki 20 > -5).
3-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 = 3, Orifni kayfiyati = 20 + 9 = 29, xursandlik koeffitsienti 29 (chunki 29 > 3).
4-kundan so’ng: Hoshimjonni kayfiyati = -5 + 8 + (-10) = -7, Orifni kayfiyati = 20 + 9 + (-100) = -71, xursandlik koeffitsienti -7 (chunki -7 > -100).
Shunday qilib, umumiy xursandlik koeffitsienti = 20 + 29 + (-7) = 42.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 7 3 -5 8 -10 3 7 -4 20 9 -100 105 20 1 6 1 5 2 4 3 3 3 6 2 5 4 5 |
120 70 42 9 55 76 -5 |
L. Muhim tugunlar #1
Xotira: 16 MB, Vaqt: 1000 ms\(N\) ta tugun va \(M\) ta qirradan iborat bog’langan yo’nalmagan graf berilgan. Ya’ni graf qirralari ikki tomonlamali hamda grafdagi ixtiyoriy tugundan boshqasiga qirralar orqali borish mumkin.
\(x\) va \(y\) tugunlar \((x \ne y)\) uchun muhim tugun deb shunaqangi \(u\) tugunga aytiladiki \((u \ne x, u \ne y)\), agar shu \(u\) tugun grafdan olib tashlansa, grafda \(x\) dan \(y\) ga borishni imkoni bo’lmay qolsin.
Sizga \(q\) ta so’rovlar orqali \(x\) va \(y\) tugunlar juftliklari beriladi, har bir so’rovdagi juftlik uchun muhim tugunlar sonini chiqaring.
Birinchi qatorda ikkita butun son tugunlar soni \(n\) va qirralar soni \(m\) kiritiladi \((3 ≤ n, m ≤ 10^5)\). Keyingi \(m\) ta qatorda graf qirralari \(u\) va \(v\) sonlar juftligi ko’rinishida beriladi \((1 ≤ u, v ≤ n, u \ne v)\).
Keyingi qatorda so’rovlar soni \(q\) beriladi \((1 ≤ q ≤ 10^5)\). Keyingi \(q\) ta qatorda so’rovlarni ifodalovchi \(x\) va \(y\) sonlar juftligi beriladi \((1 ≤ x, y ≤ n, x \ne y)\).
1-subtask (11 ball): \(n, m, q ≤ 300\).
2-subtask (9 ball): Graf to’g’ri chiziq shaklida, ya’ni har bir tugunni bitta yoki ikkita qo’shnisi bo’lishi mumkin (\(m = n - 1\) va \(n, q ≤ 10^5\)).
3-subtask (13 ball): \(m = n - 1\) hamda har bir \(i*2+1 ≤ n\) bo’lgan \(i\)-tugundan \(i*2\) va \(i*2+1\) tugunlarga qirra mavjud (\(m = n - 1\) va \(n, q ≤ 10^5\)).
4-subtask (21 ball): \(m = n - 1\) va \(n, q ≤ 10^5\)
5-subtask (46 ball): \(n, m, q ≤ 10^5\)
Har bir so’rov uchun \(x\) va \(y\) tugunlar juftligiga nisbatan muhim bo’lgan tugunlar sonini chiqaring.
Birinchi misoldagi graf quyidagicha ko’rinishda:
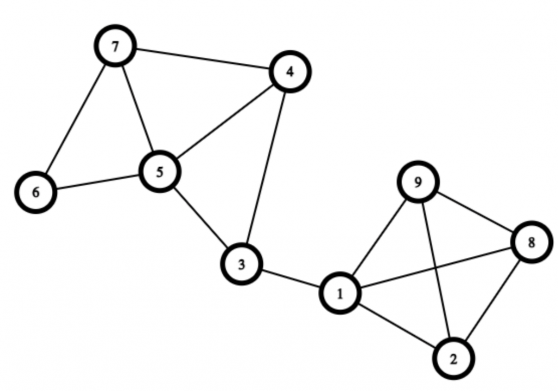
1-so’rovda 3 va 8 tugunlar uchun yagona muhim tugun 1-tugun hisoblanadi.
2-so’rovda 1-va 3- tugunlar uchun birorta ham muhim tugun yo’q, grafdagi boshqa ixtiyoriy tugunni olib tashlasa ham bu tugunlar o’rtasida yo’l doim bo’ladi.
3-so’rovda 4- va 9- tugunlar uchun muhim tugunlar 3- va 1- tugunlardir.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
9 14 4 7 5 6 5 7 6 7 1 8 1 2 1 3 3 4 3 5 4 5 1 9 2 9 2 8 9 8 3 3 8 1 3 4 9 |
1 0 2 |
M. Muhim tugunlar #2
Xotira: 16 MB, Vaqt: 1000 ms\(N\) ta tugun va \(M\) ta qirradan iborat bog’langan yo’nalmagan graf berilgan. Ya’ni graf qirralari ikki tomonlamali hamda grafdagi ixtiyoriy tugundan boshqasiga qirralar orqali borish mumkin.
\(x\) va \(y\) tugunlar \((x \ne y)\) uchun muhim tugun deb shunaqangi \(u\) tugunga aytiladiki \((u \ne x, u \ne y)\), agar shu \(u\) tugun grafdan olib tashlansa, grafda \(x\) dan \(y\) ga borishni imkoni bo’lmay qolsin.
Sizga \(q\) ta so’rovlar orqali \(x\) va \(y\) tugunlar juftliklari beriladi, har bir so’rovdagi juftlik uchun muhim tugunlar sonini chiqaring.
Birinchi qatorda ikkita butun son tugunlar soni \(n\) va qirralar soni \(m\) kiritiladi \((3 ≤ n, m ≤ 10^5)\). Keyingi \(m\) ta qatorda graf qirralari \(u\) va \(v\) sonlar juftligi ko’rinishida beriladi \((1 ≤ u, v ≤ n, u \ne v)\).
Keyingi qatorda so’rovlar soni \(q\) beriladi \((1 ≤ q ≤ 10^5)\). Keyingi \(q\) ta qatorda so’rovlarni ifodalovchi \(x\) va \(y\) sonlar juftligi beriladi \((1 ≤ x, y ≤ n, x \ne y)\).
1-subtask (11 ball): \(n, m, q ≤ 300\).
2-subtask (9 ball): Graf to’g’ri chiziq shaklida, ya’ni har bir tugunni bitta yoki ikkita qo’shnisi bo’lishi mumkin (\(m = n - 1\) va \(n, q ≤ 10^5\)).
3-subtask (13 ball): \(m = n - 1\) hamda har bir \(i*2+1 ≤ n\) bo’lgan \(i\)-tugundan \(i*2\) va \(i*2+1\) tugunlarga qirra mavjud (\(m = n - 1\) va \(n, q ≤ 10^5\)).
4-subtask (21 ball): \(m = n - 1\) va \(n, q ≤ 10^5\)
5-subtask (46 ball): \(n, m, q ≤ 10^5\)
Har bir so’rov uchun \(x\) va \(y\) tugunlar juftligiga nisbatan muhim bo’lgan tugunlar sonini chiqaring.
Birinchi misoldagi graf quyidagicha ko’rinishda:

1-so’rovda 3 va 8 tugunlar uchun yagona muhim tugun 1-tugun hisoblanadi.
2-so’rovda 1-va 3- tugunlar uchun birorta ham muhim tugun yo’q, grafdagi boshqa ixtiyoriy tugunni olib tashlasa ham bu tugunlar o’rtasida yo’l doim bo’ladi.
3-so’rovda 4- va 9- tugunlar uchun muhim tugunlar 3- va 1- tugunlardir.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
9 14 4 7 5 6 5 7 6 7 1 8 1 2 1 3 3 4 3 5 4 5 1 9 2 9 2 8 9 8 3 3 8 1 3 4 9 |
1 0 2 |
N. Muhim tugunlar #3
Xotira: 16 MB, Vaqt: 1000 ms\(N\) ta tugun va \(M\) ta qirradan iborat bog’langan yo’nalmagan graf berilgan. Ya’ni graf qirralari ikki tomonlamali hamda grafdagi ixtiyoriy tugundan boshqasiga qirralar orqali borish mumkin.
\(x\) va \(y\) tugunlar \((x \ne y)\) uchun muhim tugun deb shunaqangi \(u\) tugunga aytiladiki \((u \ne x, u \ne y)\), agar shu \(u\) tugun grafdan olib tashlansa, grafda \(x\) dan \(y\) ga borishni imkoni bo’lmay qolsin.
Sizga \(q\) ta so’rovlar orqali \(x\) va \(y\) tugunlar juftliklari beriladi, har bir so’rovdagi juftlik uchun muhim tugunlar sonini chiqaring.
Birinchi qatorda ikkita butun son tugunlar soni \(n\) va qirralar soni \(m\) kiritiladi \((3 ≤ n, m ≤ 10^5)\). Keyingi \(m\) ta qatorda graf qirralari \(u\) va \(v\) sonlar juftligi ko’rinishida beriladi \((1 ≤ u, v ≤ n, u \ne v)\).
Keyingi qatorda so’rovlar soni \(q\) beriladi \((1 ≤ q ≤ 10^5)\). Keyingi \(q\) ta qatorda so’rovlarni ifodalovchi \(x\) va \(y\) sonlar juftligi beriladi \((1 ≤ x, y ≤ n, x \ne y)\).
1-subtask (11 ball): \(n, m, q ≤ 300\).
2-subtask (9 ball): Graf to’g’ri chiziq shaklida, ya’ni har bir tugunni bitta yoki ikkita qo’shnisi bo’lishi mumkin (\(m = n - 1\) va \(n, q ≤ 10^5\)).
3-subtask (13 ball): \(m = n - 1\) hamda har bir \(i*2+1 ≤ n\) bo’lgan \(i\)-tugundan \(i*2\) va \(i*2+1\) tugunlarga qirra mavjud (\(m = n - 1\) va \(n, q ≤ 10^5\)).
4-subtask (21 ball): \(m = n - 1\) va \(n, q ≤ 10^5\)
5-subtask (46 ball): \(n, m, q ≤ 10^5\)
Har bir so’rov uchun \(x\) va \(y\) tugunlar juftligiga nisbatan muhim bo’lgan tugunlar sonini chiqaring.
Birinchi misoldagi graf quyidagicha ko’rinishda:

1-so’rovda 3 va 8 tugunlar uchun yagona muhim tugun 1-tugun hisoblanadi.
2-so’rovda 1-va 3- tugunlar uchun birorta ham muhim tugun yo’q, grafdagi boshqa ixtiyoriy tugunni olib tashlasa ham bu tugunlar o’rtasida yo’l doim bo’ladi.
3-so’rovda 4- va 9- tugunlar uchun muhim tugunlar 3- va 1- tugunlardir.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
9 14 4 7 5 6 5 7 6 7 1 8 1 2 1 3 3 4 3 5 4 5 1 9 2 9 2 8 9 8 3 3 8 1 3 4 9 |
1 0 2 |
O. Muhim tugunlar #4
Xotira: 64 MB, Vaqt: 1000 ms\(N\) ta tugun va \(M\) ta qirradan iborat bog’langan yo’nalmagan graf berilgan. Ya’ni graf qirralari ikki tomonlamali hamda grafdagi ixtiyoriy tugundan boshqasiga qirralar orqali borish mumkin.
\(x\) va \(y\) tugunlar \((x \ne y)\) uchun muhim tugun deb shunaqangi \(u\) tugunga aytiladiki \((u \ne x, u \ne y)\), agar shu \(u\) tugun grafdan olib tashlansa, grafda \(x\) dan \(y\) ga borishni imkoni bo’lmay qolsin.
Sizga \(q\) ta so’rovlar orqali \(x\) va \(y\) tugunlar juftliklari beriladi, har bir so’rovdagi juftlik uchun muhim tugunlar sonini chiqaring.
Birinchi qatorda ikkita butun son tugunlar soni \(n\) va qirralar soni \(m\) kiritiladi \((3 ≤ n, m ≤ 10^5)\). Keyingi \(m\) ta qatorda graf qirralari \(u\) va \(v\) sonlar juftligi ko’rinishida beriladi \((1 ≤ u, v ≤ n, u \ne v)\).
Keyingi qatorda so’rovlar soni \(q\) beriladi \((1 ≤ q ≤ 10^5)\). Keyingi \(q\) ta qatorda so’rovlarni ifodalovchi \(x\) va \(y\) sonlar juftligi beriladi \((1 ≤ x, y ≤ n, x \ne y)\).
1-subtask (11 ball): \(n, m, q ≤ 300\).
2-subtask (9 ball): Graf to’g’ri chiziq shaklida, ya’ni har bir tugunni bitta yoki ikkita qo’shnisi bo’lishi mumkin (\(m = n - 1\) va \(n, q ≤ 10^5\)).
3-subtask (13 ball): \(m = n - 1\) hamda har bir \(i*2+1 ≤ n\) bo’lgan \(i\)-tugundan \(i*2\) va \(i*2+1\) tugunlarga qirra mavjud (\(m = n - 1\) va \(n, q ≤ 10^5\)).
4-subtask (21 ball): \(m = n - 1\) va \(n, q ≤ 10^5\)
5-subtask (46 ball): \(n, m, q ≤ 10^5\)
Har bir so’rov uchun \(x\) va \(y\) tugunlar juftligiga nisbatan muhim bo’lgan tugunlar sonini chiqaring.
Birinchi misoldagi graf quyidagicha ko’rinishda:

1-so’rovda 3 va 8 tugunlar uchun yagona muhim tugun 1-tugun hisoblanadi.
2-so’rovda 1-va 3- tugunlar uchun birorta ham muhim tugun yo’q, grafdagi boshqa ixtiyoriy tugunni olib tashlasa ham bu tugunlar o’rtasida yo’l doim bo’ladi.
3-so’rovda 4- va 9- tugunlar uchun muhim tugunlar 3- va 1- tugunlardir.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
9 14 4 7 5 6 5 7 6 7 1 8 1 2 1 3 3 4 3 5 4 5 1 9 2 9 2 8 9 8 3 3 8 1 3 4 9 |
1 0 2 |
P. Muhim tugunlar #5
Xotira: 64 MB, Vaqt: 1000 ms\(N\) ta tugun va \(M\) ta qirradan iborat bog’langan yo’nalmagan graf berilgan. Ya’ni graf qirralari ikki tomonlamali hamda grafdagi ixtiyoriy tugundan boshqasiga qirralar orqali borish mumkin.
\(x\) va \(y\) tugunlar \((x \ne y)\) uchun muhim tugun deb shunaqangi \(u\) tugunga aytiladiki \((u \ne x, u \ne y)\), agar shu \(u\) tugun grafdan olib tashlansa, grafda \(x\) dan \(y\) ga borishni imkoni bo’lmay qolsin.
Sizga \(q\) ta so’rovlar orqali \(x\) va \(y\) tugunlar juftliklari beriladi, har bir so’rovdagi juftlik uchun muhim tugunlar sonini chiqaring.
Birinchi qatorda ikkita butun son tugunlar soni \(n\) va qirralar soni \(m\) kiritiladi \((3 ≤ n, m ≤ 10^5)\). Keyingi \(m\) ta qatorda graf qirralari \(u\) va \(v\) sonlar juftligi ko’rinishida beriladi \((1 ≤ u, v ≤ n, u \ne v)\).
Keyingi qatorda so’rovlar soni \(q\) beriladi \((1 ≤ q ≤ 10^5)\). Keyingi \(q\) ta qatorda so’rovlarni ifodalovchi \(x\) va \(y\) sonlar juftligi beriladi \((1 ≤ x, y ≤ n, x \ne y)\).
1-subtask (11 ball): \(n, m, q ≤ 300\).
2-subtask (9 ball): Graf to’g’ri chiziq shaklida, ya’ni har bir tugunni bitta yoki ikkita qo’shnisi bo’lishi mumkin (\(m = n - 1\) va \(n, q ≤ 10^5\)).
3-subtask (13 ball): \(m = n - 1\) hamda har bir \(i*2+1 ≤ n\) bo’lgan \(i\)-tugundan \(i*2\) va \(i*2+1\) tugunlarga qirra mavjud (\(m = n - 1\) va \(n, q ≤ 10^5\)).
4-subtask (21 ball): \(m = n - 1\) va \(n, q ≤ 10^5\)
5-subtask (46 ball): \(n, m, q ≤ 10^5\)
Har bir so’rov uchun \(x\) va \(y\) tugunlar juftligiga nisbatan muhim bo’lgan tugunlar sonini chiqaring.
Birinchi misoldagi graf quyidagicha ko’rinishda:

1-so’rovda 3 va 8 tugunlar uchun yagona muhim tugun 1-tugun hisoblanadi.
2-so’rovda 1-va 3- tugunlar uchun birorta ham muhim tugun yo’q, grafdagi boshqa ixtiyoriy tugunni olib tashlasa ham bu tugunlar o’rtasida yo’l doim bo’ladi.
3-so’rovda 4- va 9- tugunlar uchun muhim tugunlar 3- va 1- tugunlardir.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
9 14 4 7 5 6 5 7 6 7 1 8 1 2 1 3 3 4 3 5 4 5 1 9 2 9 2 8 9 8 3 3 8 1 3 4 9 |
1 0 2 |