A. Tug’ilgan kun #1
Xotira: 16 MB, Vaqt: 1000 msAkrom bugun tug’ilgan kunini nishonlamoqda va shu munosabat bilan o’zining \(k\) ta do’stini kechki ovqatga taklif qildi. Kechki ovqat stolida bir qatorda terilgan \(n\) ta ovqat bo’lib, \(i\)- ovqatni yegan odamni kayfiyati \(a_i\) ga o’zgaradi. Endi Akrom bu ovqatlarni do’stlariga bo’lib berishi kerak.
Har bir mehmon stolda ketma-ket joylashgan bir nechta ovqatni yeyishi yoki umuman ovqat yemasligi ham mumkin. Ammo bitta ovqatni faqat bir kishi yeya oladi xolos. Akrom mehmonlarga ovqatlarni shunaqangi bo’lib berishi kerakki, ovqatlanib bo’lgandan so’ng mehmonlarning umumiy kayfiyati maksimal bo’lsin. Bunda Akromga yordam bering.
Birinchi qatorda ovqatlar soni \(n\) va mehmonlar soni \(k\) kiritiladi \((1 ≤ k ≤ n ≤ 10^5)\). Keyingi qatorda \(n\) ta butun son - \(a_1, a_2, ..., a_n\) kiritiladi \((-10^9 ≤ a_i ≤ 10^9)\).
1-subtask(5 ball): \(a_i ≥ 0, n ≤ 10^5\)
2-subtask(6 ball): Ko’pi bilan bitta ovqat uchun \(a_i ≤ 0\) bo’ladi, \(n ≤ 10^5\)
3-subtask(10 ball): \(k = 1\)
4-subtask(15 ball): \(1 ≤ k ≤ n ≤ 80\)
5-subtask(26 ball): \(1 ≤ k ≤ n ≤ 2000\)
6-subtask(38 ball): \(1 ≤ k ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda yagona mehmon uchun [3, -1, 5] oraliqni bersak optimal bo’ladi.
Ikkinchi misolda 2 ta mehmonlar uchun [1, 2, 3] va [5, 6] oraliqdagi ovqatlarni bersak, ularning umumiy kayfiyati 6 + 11 = 17 bo’ladi.
Uchinchi misolda hech qaysi mehmonga ovqat bermagan ma’qul.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 1 -2 3 -1 5 -6 |
7 |
| 2 |
6 2 1 2 3 -10 5 6 |
17 |
| 3 |
6 4 -1 -2 -1 0 -5 -1 |
0 |
B. Tug’ilgan kun #2
Xotira: 16 MB, Vaqt: 1000 msAkrom bugun tug’ilgan kunini nishonlamoqda va shu munosabat bilan o’zining \(k\) ta do’stini kechki ovqatga taklif qildi. Kechki ovqat stolida bir qatorda terilgan \(n\) ta ovqat bo’lib, \(i\)- ovqatni yegan odamni kayfiyati \(a_i\) ga o’zgaradi. Endi Akrom bu ovqatlarni do’stlariga bo’lib berishi kerak.
Har bir mehmon stolda ketma-ket joylashgan bir nechta ovqatni yeyishi yoki umuman ovqat yemasligi ham mumkin. Ammo bitta ovqatni faqat bir kishi yeya oladi xolos. Akrom mehmonlarga ovqatlarni shunaqangi bo’lib berishi kerakki, ovqatlanib bo’lgandan so’ng mehmonlarning umumiy kayfiyati maksimal bo’lsin. Bunda Akromga yordam bering.
Birinchi qatorda ovqatlar soni \(n\) va mehmonlar soni \(k\) kiritiladi \((1 ≤ k ≤ n ≤ 10^5)\). Keyingi qatorda \(n\) ta butun son - \(a_1, a_2, ..., a_n\) kiritiladi \((-10^9 ≤ a_i ≤ 10^9)\).
1-subtask(5 ball): \(a_i ≥ 0, n ≤ 10^5\)
2-subtask(6 ball): Ko’pi bilan bitta ovqat uchun \(a_i ≤ 0\) bo’ladi, \(n ≤ 10^5\)
3-subtask(10 ball): \(k = 1\)
4-subtask(15 ball): \(1 ≤ k ≤ n ≤ 80\)
5-subtask(26 ball): \(1 ≤ k ≤ n ≤ 2000\)
6-subtask(38 ball): \(1 ≤ k ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda yagona mehmon uchun [3, -1, 5] oraliqni bersak optimal bo’ladi.
Ikkinchi misolda 2 ta mehmonlar uchun [1, 2, 3] va [5, 6] oraliqdagi ovqatlarni bersak, ularning umumiy kayfiyati 6 + 11 = 17 bo’ladi.
Uchinchi misolda hech qaysi mehmonga ovqat bermagan ma’qul.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 1 -2 3 -1 5 -6 |
7 |
| 2 |
6 2 1 2 3 -10 5 6 |
17 |
| 3 |
6 4 -1 -2 -1 0 -5 -1 |
0 |
C. Tug’ilgan kun #3
Xotira: 16 MB, Vaqt: 1000 msAkrom bugun tug’ilgan kunini nishonlamoqda va shu munosabat bilan o’zining \(k\) ta do’stini kechki ovqatga taklif qildi. Kechki ovqat stolida bir qatorda terilgan \(n\) ta ovqat bo’lib, \(i\)- ovqatni yegan odamni kayfiyati \(a_i\) ga o’zgaradi. Endi Akrom bu ovqatlarni do’stlariga bo’lib berishi kerak.
Har bir mehmon stolda ketma-ket joylashgan bir nechta ovqatni yeyishi yoki umuman ovqat yemasligi ham mumkin. Ammo bitta ovqatni faqat bir kishi yeya oladi xolos. Akrom mehmonlarga ovqatlarni shunaqangi bo’lib berishi kerakki, ovqatlanib bo’lgandan so’ng mehmonlarning umumiy kayfiyati maksimal bo’lsin. Bunda Akromga yordam bering.
Birinchi qatorda ovqatlar soni \(n\) va mehmonlar soni \(k\) kiritiladi \((1 ≤ k ≤ n ≤ 10^5)\). Keyingi qatorda \(n\) ta butun son - \(a_1, a_2, ..., a_n\) kiritiladi \((-10^9 ≤ a_i ≤ 10^9)\).
1-subtask(5 ball): \(a_i ≥ 0, n ≤ 10^5\)
2-subtask(6 ball): Ko’pi bilan bitta ovqat uchun \(a_i ≤ 0\) bo’ladi, \(n ≤ 10^5\)
3-subtask(10 ball): \(k = 1\)
4-subtask(15 ball): \(1 ≤ k ≤ n ≤ 80\)
5-subtask(26 ball): \(1 ≤ k ≤ n ≤ 2000\)
6-subtask(38 ball): \(1 ≤ k ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda yagona mehmon uchun [3, -1, 5] oraliqni bersak optimal bo’ladi.
Ikkinchi misolda 2 ta mehmonlar uchun [1, 2, 3] va [5, 6] oraliqdagi ovqatlarni bersak, ularning umumiy kayfiyati 6 + 11 = 17 bo’ladi.
Uchinchi misolda hech qaysi mehmonga ovqat bermagan ma’qul.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 1 -2 3 -1 5 -6 |
7 |
| 2 |
6 2 1 2 3 -10 5 6 |
17 |
| 3 |
6 4 -1 -2 -1 0 -5 -1 |
0 |
D. Tug’ilgan kun #4
Xotira: 16 MB, Vaqt: 1000 msAkrom bugun tug’ilgan kunini nishonlamoqda va shu munosabat bilan o’zining \(k\) ta do’stini kechki ovqatga taklif qildi. Kechki ovqat stolida bir qatorda terilgan \(n\) ta ovqat bo’lib, \(i\)- ovqatni yegan odamni kayfiyati \(a_i\) ga o’zgaradi. Endi Akrom bu ovqatlarni do’stlariga bo’lib berishi kerak.
Har bir mehmon stolda ketma-ket joylashgan bir nechta ovqatni yeyishi yoki umuman ovqat yemasligi ham mumkin. Ammo bitta ovqatni faqat bir kishi yeya oladi xolos. Akrom mehmonlarga ovqatlarni shunaqangi bo’lib berishi kerakki, ovqatlanib bo’lgandan so’ng mehmonlarning umumiy kayfiyati maksimal bo’lsin. Bunda Akromga yordam bering.
Birinchi qatorda ovqatlar soni \(n\) va mehmonlar soni \(k\) kiritiladi \((1 ≤ k ≤ n ≤ 10^5)\). Keyingi qatorda \(n\) ta butun son - \(a_1, a_2, ..., a_n\) kiritiladi \((-10^9 ≤ a_i ≤ 10^9)\).
1-subtask(5 ball): \(a_i ≥ 0, n ≤ 10^5\)
2-subtask(6 ball): Ko’pi bilan bitta ovqat uchun \(a_i ≤ 0\) bo’ladi, \(n ≤ 10^5\)
3-subtask(10 ball): \(k = 1\)
4-subtask(15 ball): \(1 ≤ k ≤ n ≤ 80\)
5-subtask(26 ball): \(1 ≤ k ≤ n ≤ 2000\)
6-subtask(38 ball): \(1 ≤ k ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda yagona mehmon uchun [3, -1, 5] oraliqni bersak optimal bo’ladi.
Ikkinchi misolda 2 ta mehmonlar uchun [1, 2, 3] va [5, 6] oraliqdagi ovqatlarni bersak, ularning umumiy kayfiyati 6 + 11 = 17 bo’ladi.
Uchinchi misolda hech qaysi mehmonga ovqat bermagan ma’qul.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 1 -2 3 -1 5 -6 |
7 |
| 2 |
6 2 1 2 3 -10 5 6 |
17 |
| 3 |
6 4 -1 -2 -1 0 -5 -1 |
0 |
E. Tug’ilgan kun #5
Xotira: 16 MB, Vaqt: 1000 msAkrom bugun tug’ilgan kunini nishonlamoqda va shu munosabat bilan o’zining \(k\) ta do’stini kechki ovqatga taklif qildi. Kechki ovqat stolida bir qatorda terilgan \(n\) ta ovqat bo’lib, \(i\)- ovqatni yegan odamni kayfiyati \(a_i\) ga o’zgaradi. Endi Akrom bu ovqatlarni do’stlariga bo’lib berishi kerak.
Har bir mehmon stolda ketma-ket joylashgan bir nechta ovqatni yeyishi yoki umuman ovqat yemasligi ham mumkin. Ammo bitta ovqatni faqat bir kishi yeya oladi xolos. Akrom mehmonlarga ovqatlarni shunaqangi bo’lib berishi kerakki, ovqatlanib bo’lgandan so’ng mehmonlarning umumiy kayfiyati maksimal bo’lsin. Bunda Akromga yordam bering.
Birinchi qatorda ovqatlar soni \(n\) va mehmonlar soni \(k\) kiritiladi \((1 ≤ k ≤ n ≤ 10^5)\). Keyingi qatorda \(n\) ta butun son - \(a_1, a_2, ..., a_n\) kiritiladi \((-10^9 ≤ a_i ≤ 10^9)\).
1-subtask(5 ball): \(a_i ≥ 0, n ≤ 10^5\)
2-subtask(6 ball): Ko’pi bilan bitta ovqat uchun \(a_i ≤ 0\) bo’ladi, \(n ≤ 10^5\)
3-subtask(10 ball): \(k = 1\)
4-subtask(15 ball): \(1 ≤ k ≤ n ≤ 80\)
5-subtask(26 ball): \(1 ≤ k ≤ n ≤ 2000\)
6-subtask(38 ball): \(1 ≤ k ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda yagona mehmon uchun [3, -1, 5] oraliqni bersak optimal bo’ladi.
Ikkinchi misolda 2 ta mehmonlar uchun [1, 2, 3] va [5, 6] oraliqdagi ovqatlarni bersak, ularning umumiy kayfiyati 6 + 11 = 17 bo’ladi.
Uchinchi misolda hech qaysi mehmonga ovqat bermagan ma’qul.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 1 -2 3 -1 5 -6 |
7 |
| 2 |
6 2 1 2 3 -10 5 6 |
17 |
| 3 |
6 4 -1 -2 -1 0 -5 -1 |
0 |
F. Tug’ilgan kun #6
Xotira: 16 MB, Vaqt: 1000 msAkrom bugun tug’ilgan kunini nishonlamoqda va shu munosabat bilan o’zining \(k\) ta do’stini kechki ovqatga taklif qildi. Kechki ovqat stolida bir qatorda terilgan \(n\) ta ovqat bo’lib, \(i\)- ovqatni yegan odamni kayfiyati \(a_i\) ga o’zgaradi. Endi Akrom bu ovqatlarni do’stlariga bo’lib berishi kerak.
Har bir mehmon stolda ketma-ket joylashgan bir nechta ovqatni yeyishi yoki umuman ovqat yemasligi ham mumkin. Ammo bitta ovqatni faqat bir kishi yeya oladi xolos. Akrom mehmonlarga ovqatlarni shunaqangi bo’lib berishi kerakki, ovqatlanib bo’lgandan so’ng mehmonlarning umumiy kayfiyati maksimal bo’lsin. Bunda Akromga yordam bering.
Birinchi qatorda ovqatlar soni \(n\) va mehmonlar soni \(k\) kiritiladi \((1 ≤ k ≤ n ≤ 10^5)\). Keyingi qatorda \(n\) ta butun son - \(a_1, a_2, ..., a_n\) kiritiladi \((-10^9 ≤ a_i ≤ 10^9)\).
1-subtask(5 ball): \(a_i ≥ 0, n ≤ 10^5\)
2-subtask(6 ball): Ko’pi bilan bitta ovqat uchun \(a_i ≤ 0\) bo’ladi, \(n ≤ 10^5\)
3-subtask(10 ball): \(k = 1\)
4-subtask(15 ball): \(1 ≤ k ≤ n ≤ 80\)
5-subtask(26 ball): \(1 ≤ k ≤ n ≤ 2000\)
6-subtask(38 ball): \(1 ≤ k ≤ n ≤ 10^5\)
Bitta butun son - masalaning javobini chiqaring.
Birinchi misolda yagona mehmon uchun [3, -1, 5] oraliqni bersak optimal bo’ladi.
Ikkinchi misolda 2 ta mehmonlar uchun [1, 2, 3] va [5, 6] oraliqdagi ovqatlarni bersak, ularning umumiy kayfiyati 6 + 11 = 17 bo’ladi.
Uchinchi misolda hech qaysi mehmonga ovqat bermagan ma’qul.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 1 -2 3 -1 5 -6 |
7 |
| 2 |
6 2 1 2 3 -10 5 6 |
17 |
| 3 |
6 4 -1 -2 -1 0 -5 -1 |
0 |
G. Daraxtni bo’yash #1
Xotira: 16 MB, Vaqt: 1000 ms\(n\) ta tugundan iborat ildizga ega binar daraxt berilgan (rooted binary tree). Ya’ni daraxtning har bir tugunini ko’pi bilan ikkita bolasi bo’lishi mumkin.
Berilgan daraxtda iloji boricha ko’p tugunlarni bo’yash kerakki, bo’yalganidan so’ng daraxt muvozanatlangan bo’lib qolsin.
Muvozanatlangan daraxt deb quyidagi shartni qanoatlantiruvchi daraxtga aytiladi:
- har bir ikkita bolasi bor \(u\) tugun uchun, shu bolalarini \(x\) va \(y\) bilan belgilaydigan bo’lsak, ildizi \(x\) da bo’lgan va ildizi \(y\) da bo’lgan qism daraxtlardagi bo’yalgan tugunlar soni teng bo’lsin.
Masalan, quyidagi daraxt muvozanatlangan daraxtga misol bo’la oladi:
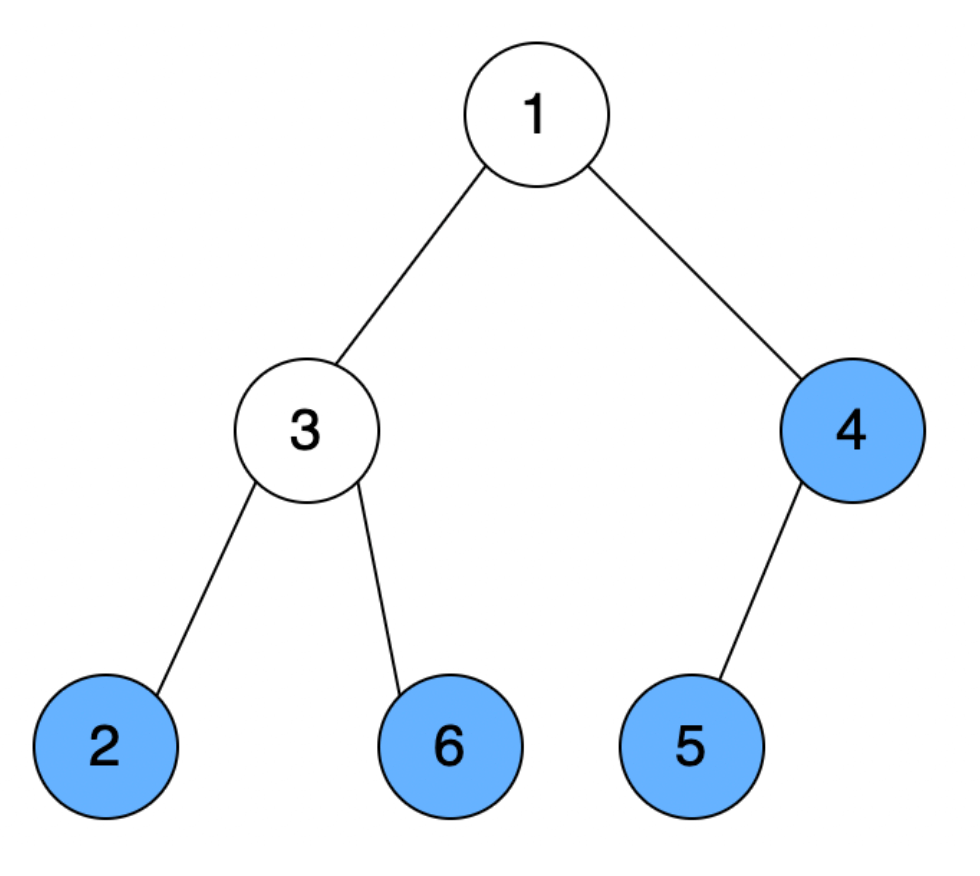
- 3-tugunni ikkala bolasidagi qism daraxtda 1 tadan bo’yalgan tugun bor.
- 1-tugunni ikkala bolasidagi qism daraxtda 2 tadan bo’yalgan tugun bor.
- 4-tugunni bolalari soni 1 ta bo’lgani sabab, uni e’tiborga olish shart emas.
Birinchi qatorda tugunlar soni \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda daraxt qirralarini ifodalovchi \(n - 1\) ta \(u\) va \(v\) ko’rinishidagi sonlar juftligi beriladi \((1 ≤ u, v ≤ n, u \ne v)\). Daraxt ildizi doim 1-tugun bo’ladi.
1-subtask(9 ball): Har bir tugunning ko’pi bilan bitta bolasi bor, \(n ≤ 100\)
2-subtask(20 ball): \(n ≤ 15\)
3-subtask(31 ball): Har bir tugunning 0 ta yoki 2 ta bolasi bor \(n ≤ 10^5\)
4-subtask(40 ball): \(n ≤ 10^5\)
Bitta butun son - bo’yash mumkin bo’lgan maksimal tugunlar sonini chiqaring.
Birinchi misoldagi daraxt yuqoridagi rasmda keltirilgan. Faqat qo’shimchasiga 1-tugunni ham bo’yash imkoni bor, shuning uchun javob 5.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 3 4 1 3 2 6 3 4 5 |
5 |
H. Daraxtni bo’yash #2
Xotira: 16 MB, Vaqt: 1000 ms\(n\) ta tugundan iborat ildizga ega binar daraxt berilgan (rooted binary tree). Ya’ni daraxtning har bir tugunini ko’pi bilan ikkita bolasi bo’lishi mumkin.
Berilgan daraxtda iloji boricha ko’p tugunlarni bo’yash kerakki, bo’yalganidan so’ng daraxt muvozanatlangan bo’lib qolsin.
Muvozanatlangan daraxt deb quyidagi shartni qanoatlantiruvchi daraxtga aytiladi:
- har bir ikkita bolasi bor \(u\) tugun uchun, shu bolalarini \(x\) va \(y\) bilan belgilaydigan bo’lsak, ildizi \(x\) da bo’lgan va ildizi \(y\) da bo’lgan qism daraxtlardagi bo’yalgan tugunlar soni teng bo’lsin.
Masalan, quyidagi daraxt muvozanatlangan daraxtga misol bo’la oladi:

- 3-tugunni ikkala bolasidagi qism daraxtda 1 tadan bo’yalgan tugun bor.
- 1-tugunni ikkala bolasidagi qism daraxtda 2 tadan bo’yalgan tugun bor.
- 4-tugunni bolalari soni 1 ta bo’lgani sabab, uni e’tiborga olish shart emas.
Birinchi qatorda tugunlar soni \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda daraxt qirralarini ifodalovchi \(n - 1\) ta \(u\) va \(v\) ko’rinishidagi sonlar juftligi beriladi \((1 ≤ u, v ≤ n, u \ne v)\). Daraxt ildizi doim 1-tugun bo’ladi.
1-subtask(9 ball): Har bir tugunning ko’pi bilan bitta bolasi bor, \(n ≤ 100\)
2-subtask(20 ball): \(n ≤ 15\)
3-subtask(31 ball): Har bir tugunning 0 ta yoki 2 ta bolasi bor \(n ≤ 10^5\)
4-subtask(40 ball): \(n ≤ 10^5\)
Bitta butun son - bo’yash mumkin bo’lgan maksimal tugunlar sonini chiqaring.
Birinchi misoldagi daraxt yuqoridagi rasmda keltirilgan. Faqat qo’shimchasiga 1-tugunni ham bo’yash imkoni bor, shuning uchun javob 5.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 3 4 1 3 2 6 3 4 5 |
5 |
I. Daraxtni bo’yash #3
Xotira: 16 MB, Vaqt: 1000 ms\(n\) ta tugundan iborat ildizga ega binar daraxt berilgan (rooted binary tree). Ya’ni daraxtning har bir tugunini ko’pi bilan ikkita bolasi bo’lishi mumkin.
Berilgan daraxtda iloji boricha ko’p tugunlarni bo’yash kerakki, bo’yalganidan so’ng daraxt muvozanatlangan bo’lib qolsin.
Muvozanatlangan daraxt deb quyidagi shartni qanoatlantiruvchi daraxtga aytiladi:
- har bir ikkita bolasi bor \(u\) tugun uchun, shu bolalarini \(x\) va \(y\) bilan belgilaydigan bo’lsak, ildizi \(x\) da bo’lgan va ildizi \(y\) da bo’lgan qism daraxtlardagi bo’yalgan tugunlar soni teng bo’lsin.
Masalan, quyidagi daraxt muvozanatlangan daraxtga misol bo’la oladi:

- 3-tugunni ikkala bolasidagi qism daraxtda 1 tadan bo’yalgan tugun bor.
- 1-tugunni ikkala bolasidagi qism daraxtda 2 tadan bo’yalgan tugun bor.
- 4-tugunni bolalari soni 1 ta bo’lgani sabab, uni e’tiborga olish shart emas.
Birinchi qatorda tugunlar soni \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda daraxt qirralarini ifodalovchi \(n - 1\) ta \(u\) va \(v\) ko’rinishidagi sonlar juftligi beriladi \((1 ≤ u, v ≤ n, u \ne v)\). Daraxt ildizi doim 1-tugun bo’ladi.
1-subtask(9 ball): Har bir tugunning ko’pi bilan bitta bolasi bor, \(n ≤ 100\)
2-subtask(20 ball): \(n ≤ 15\)
3-subtask(31 ball): Har bir tugunning 0 ta yoki 2 ta bolasi bor \(n ≤ 10^5\)
4-subtask(40 ball): \(n ≤ 10^5\)
Bitta butun son - bo’yash mumkin bo’lgan maksimal tugunlar sonini chiqaring.
Birinchi misoldagi daraxt yuqoridagi rasmda keltirilgan. Faqat qo’shimchasiga 1-tugunni ham bo’yash imkoni bor, shuning uchun javob 5.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 3 4 1 3 2 6 3 4 5 |
5 |
J. Daraxtni bo’yash #4
Xotira: 16 MB, Vaqt: 1000 ms\(n\) ta tugundan iborat ildizga ega binar daraxt berilgan (rooted binary tree). Ya’ni daraxtning har bir tugunini ko’pi bilan ikkita bolasi bo’lishi mumkin.
Berilgan daraxtda iloji boricha ko’p tugunlarni bo’yash kerakki, bo’yalganidan so’ng daraxt muvozanatlangan bo’lib qolsin.
Muvozanatlangan daraxt deb quyidagi shartni qanoatlantiruvchi daraxtga aytiladi:
- har bir ikkita bolasi bor \(u\) tugun uchun, shu bolalarini \(x\) va \(y\) bilan belgilaydigan bo’lsak, ildizi \(x\) da bo’lgan va ildizi \(y\) da bo’lgan qism daraxtlardagi bo’yalgan tugunlar soni teng bo’lsin.
Masalan, quyidagi daraxt muvozanatlangan daraxtga misol bo’la oladi:

- 3-tugunni ikkala bolasidagi qism daraxtda 1 tadan bo’yalgan tugun bor.
- 1-tugunni ikkala bolasidagi qism daraxtda 2 tadan bo’yalgan tugun bor.
- 4-tugunni bolalari soni 1 ta bo’lgani sabab, uni e’tiborga olish shart emas.
Birinchi qatorda tugunlar soni \(n\) kiritiladi \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda daraxt qirralarini ifodalovchi \(n - 1\) ta \(u\) va \(v\) ko’rinishidagi sonlar juftligi beriladi \((1 ≤ u, v ≤ n, u \ne v)\). Daraxt ildizi doim 1-tugun bo’ladi.
1-subtask(9 ball): Har bir tugunning ko’pi bilan bitta bolasi bor, \(n ≤ 100\)
2-subtask(20 ball): \(n ≤ 15\)
3-subtask(31 ball): Har bir tugunning 0 ta yoki 2 ta bolasi bor \(n ≤ 10^5\)
4-subtask(40 ball): \(n ≤ 10^5\)
Bitta butun son - bo’yash mumkin bo’lgan maksimal tugunlar sonini chiqaring.
Birinchi misoldagi daraxt yuqoridagi rasmda keltirilgan. Faqat qo’shimchasiga 1-tugunni ham bo’yash imkoni bor, shuning uchun javob 5.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 3 4 1 3 2 6 3 4 5 |
5 |
K. Kesishmalar #1
Xotira: 16 MB, Vaqt: 1000 ms1 dan \(2n\) gacha raqamlangan nuqtalar aylana atrofida soat strelkasi bo’ylab joylashgan. Nuqtalarning aniq \(n\) tasi qora, \(n\) tasi oq.
Quyidagi shartlarni qanoatlantiruvchi \(n\) ta kesma chizamiz:
- har bir kesma qaysidir oq va qaysidir qora nuqtalarni ulaydi.
- har bir nuqtaga ko’pi bilan bitta kesma ulanishi mumkin.
Sizning vazifangiz shu kabi \(n\) ta kesmani chizish orqali maksimal kesishish koeffitsientiga erishishdan iborat. Kesishish koeffitsienti bir biri bilan kesishadigan kesmalar juftliklari soniga teng.
Birinchi qatorda bitta butun \(n\) soni \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda uzunligi \(2n\) bo’lgan B va W harflaridan iborat \(S\) satr beriladi, satrning \(i\)-belgisi\((1 ≤ i ≤ 2n)\) B bo’lsa, \(i\)- nuqta qoraligini, W bo’lsa oqligini bildiradi.
1-subtask(9 ball) Aylanada dastlab \(n\) ta qora nuqta, so’ng \(n\) ta oq nuqta joylashgan, \(n ≤ 100\)
2-subtask(15 ball): \(n ≤ 8\).
3-subtask(31 ball): \(n ≤ 300\).
4-subtask(45 ball): \(n ≤ 10^5\).
Bitta butun son - masalaning javobini chiqaring.
Birinchi misol uchun kesmalarni chap tomondagi rasmdagi kabi o’tqizadigan bo’lsak, kesishish koeffitsienti 2 bo’ladi. O’ng tomondagi rasmda esa, kesishmalar soni 3 ta bo’lishiga qaramay, 2- va 5- nuqtalardan o’tuvchi va 6- va 3- nuqtalardan o’tuvchi kesmalar masala shartiga to’g’ri kelmaydi, chunki kesmaning ikki tarafidagi nuqtalar oq va qora rangda bo’lishi lozim.
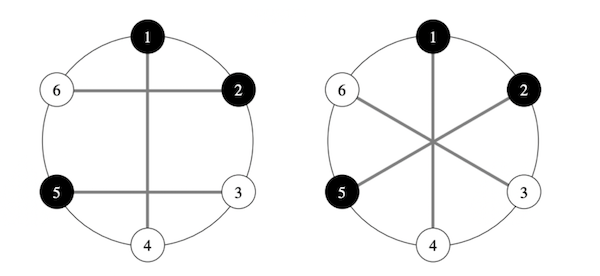
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 BBWWBW |
2 |
| 2 |
5 BWBWBBWBWW |
8 |
L. Kesishmalar #2
Xotira: 16 MB, Vaqt: 1000 ms1 dan \(2n\) gacha raqamlangan nuqtalar aylana atrofida soat strelkasi bo’ylab joylashgan. Nuqtalarning aniq \(n\) tasi qora, \(n\) tasi oq.
Quyidagi shartlarni qanoatlantiruvchi \(n\) ta kesma chizamiz:
- har bir kesma qaysidir oq va qaysidir qora nuqtalarni ulaydi.
- har bir nuqtaga ko’pi bilan bitta kesma ulanishi mumkin.
Sizning vazifangiz shu kabi \(n\) ta kesmani chizish orqali maksimal kesishish koeffitsientiga erishishdan iborat. Kesishish koeffitsienti bir biri bilan kesishadigan kesmalar juftliklari soniga teng.
Birinchi qatorda bitta butun \(n\) soni \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda uzunligi \(2n\) bo’lgan B va W harflaridan iborat \(S\) satr beriladi, satrning \(i\)-belgisi\((1 ≤ i ≤ 2n)\) B bo’lsa, \(i\)- nuqta qoraligini, W bo’lsa oqligini bildiradi.
1-subtask(9 ball) Aylanada dastlab \(n\) ta qora nuqta, so’ng \(n\) ta oq nuqta joylashgan, \(n ≤ 100\)
2-subtask(15 ball): \(n ≤ 8\).
3-subtask(31 ball): \(n ≤ 300\).
4-subtask(45 ball): \(n ≤ 10^5\).
Bitta butun son - masalaning javobini chiqaring.
Birinchi misol uchun kesmalarni chap tomondagi rasmdagi kabi o’tqizadigan bo’lsak, kesishish koeffitsienti 2 bo’ladi. O’ng tomondagi rasmda esa, kesishmalar soni 3 ta bo’lishiga qaramay, 2- va 5- nuqtalardan o’tuvchi va 6- va 3- nuqtalardan o’tuvchi kesmalar masala shartiga to’g’ri kelmaydi, chunki kesmaning ikki tarafidagi nuqtalar oq va qora rangda bo’lishi lozim.

| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 BBWWBW |
2 |
| 2 |
5 BWBWBBWBWW |
8 |
M. Kesishmalar #3
Xotira: 16 MB, Vaqt: 1000 ms1 dan \(2n\) gacha raqamlangan nuqtalar aylana atrofida soat strelkasi bo’ylab joylashgan. Nuqtalarning aniq \(n\) tasi qora, \(n\) tasi oq.
Quyidagi shartlarni qanoatlantiruvchi \(n\) ta kesma chizamiz:
- har bir kesma qaysidir oq va qaysidir qora nuqtalarni ulaydi.
- har bir nuqtaga ko’pi bilan bitta kesma ulanishi mumkin.
Sizning vazifangiz shu kabi \(n\) ta kesmani chizish orqali maksimal kesishish koeffitsientiga erishishdan iborat. Kesishish koeffitsienti bir biri bilan kesishadigan kesmalar juftliklari soniga teng.
Birinchi qatorda bitta butun \(n\) soni \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda uzunligi \(2n\) bo’lgan B va W harflaridan iborat \(S\) satr beriladi, satrning \(i\)-belgisi\((1 ≤ i ≤ 2n)\) B bo’lsa, \(i\)- nuqta qoraligini, W bo’lsa oqligini bildiradi.
1-subtask(9 ball) Aylanada dastlab \(n\) ta qora nuqta, so’ng \(n\) ta oq nuqta joylashgan, \(n ≤ 100\)
2-subtask(15 ball): \(n ≤ 8\).
3-subtask(31 ball): \(n ≤ 300\).
4-subtask(45 ball): \(n ≤ 10^5\).
Bitta butun son - masalaning javobini chiqaring.
Birinchi misol uchun kesmalarni chap tomondagi rasmdagi kabi o’tqizadigan bo’lsak, kesishish koeffitsienti 2 bo’ladi. O’ng tomondagi rasmda esa, kesishmalar soni 3 ta bo’lishiga qaramay, 2- va 5- nuqtalardan o’tuvchi va 6- va 3- nuqtalardan o’tuvchi kesmalar masala shartiga to’g’ri kelmaydi, chunki kesmaning ikki tarafidagi nuqtalar oq va qora rangda bo’lishi lozim.

| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 BBWWBW |
2 |
| 2 |
5 BWBWBBWBWW |
8 |
N. Kesishmalar #4
Xotira: 16 MB, Vaqt: 1000 ms1 dan \(2n\) gacha raqamlangan nuqtalar aylana atrofida soat strelkasi bo’ylab joylashgan. Nuqtalarning aniq \(n\) tasi qora, \(n\) tasi oq.
Quyidagi shartlarni qanoatlantiruvchi \(n\) ta kesma chizamiz:
- har bir kesma qaysidir oq va qaysidir qora nuqtalarni ulaydi.
- har bir nuqtaga ko’pi bilan bitta kesma ulanishi mumkin.
Sizning vazifangiz shu kabi \(n\) ta kesmani chizish orqali maksimal kesishish koeffitsientiga erishishdan iborat. Kesishish koeffitsienti bir biri bilan kesishadigan kesmalar juftliklari soniga teng.
Birinchi qatorda bitta butun \(n\) soni \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda uzunligi \(2n\) bo’lgan B va W harflaridan iborat \(S\) satr beriladi, satrning \(i\)-belgisi\((1 ≤ i ≤ 2n)\) B bo’lsa, \(i\)- nuqta qoraligini, W bo’lsa oqligini bildiradi.
1-subtask(9 ball) Aylanada dastlab \(n\) ta qora nuqta, so’ng \(n\) ta oq nuqta joylashgan, \(n ≤ 100\)
2-subtask(15 ball): \(n ≤ 8\).
3-subtask(31 ball): \(n ≤ 300\).
4-subtask(45 ball): \(n ≤ 10^5\).
Bitta butun son - masalaning javobini chiqaring.
Birinchi misol uchun kesmalarni chap tomondagi rasmdagi kabi o’tqizadigan bo’lsak, kesishish koeffitsienti 2 bo’ladi. O’ng tomondagi rasmda esa, kesishmalar soni 3 ta bo’lishiga qaramay, 2- va 5- nuqtalardan o’tuvchi va 6- va 3- nuqtalardan o’tuvchi kesmalar masala shartiga to’g’ri kelmaydi, chunki kesmaning ikki tarafidagi nuqtalar oq va qora rangda bo’lishi lozim.

| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 BBWWBW |
2 |
| 2 |
5 BWBWBBWBWW |
8 |