A. Bilag'onlar
Xotira: 16 MB, Vaqt: 1000 msXonada qanchadir odam bor. Ulardan \(n\) tasi faqat ingliz tilini, \(m\) tasi ingliz tilini, \(h\) tasi ingliz va xitoy tilini, \(f\) tasi ingliz va o'zbek tilini bilishar ekan. Qancha odam bu tillardan hammasini biladi?
Kirish faylining birinchi satrida natural \(n , m , h , f\) sonlari beriladi.
Masala javobini chop eting. Agar masala javobi manfiy son chiqsa, ya'ni mavjud bo'lmasa \(-1\) chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 9 7 8 |
7 |
B. Subway Surf
Xotira: 65 MB, Vaqt: 1000 msYaqinda Qulmamat play store dan yangi Subway Surf nomli o'yin yuklab oldi.
O'yin qahramoni tunnelning bir tarafida joylashgan ya'ni \((i,1)\) koordinatada va u tunnelning nargi tarafiga o'tib olishi kerak bo'ladi \((i,m)\) koordinataga. Tunnel \(n\times m\) o'lchamli maydon deb qarash mumkun. Tunneldagi barcha poyizdlarning tezliklari bir xil bo'lib o'ngdan chapga harakat qilmoqda.
Dastlab Qulmamat o'yinni boshlaydi, u dastab \((i,j)\) koordinatada bir soniyada \((i,j+1)\) koordinataga siljiydi, oldinga siljib bo'lgandan so'ng yuqoridagi yoki pastdagi qo'shni koordinataning biriga bir birlik siljib o'tishi mumkun(joyida qolishi ham mumkun). Kiyin esa barcha poyizdlar o'ngdan chapga 2 birlik siljiydi. Qulmamat va poyizdlar uchun bu harakat navbat bilan takrorlanadi.
Agarda tunnelning oxirgi ustuniga yetib kelaolsa u g'olib bo'ladi. Sizning vazifangiz Qulmamat o'yinda g'olib bo'ladimi yo'qmi aniqlash.
Kirish faylining birinchi satrida \(t(1\leq t\leq 10)\) testlar soni. Kiyingi satrda \(t\) ta test berilgan.
Ikkita \(n,m(n=3;1\leq m\leq 100)\) tunnelning o'lchami va \(n\) ta satrda \(m\) tadan belgi, ya'ni tunnel maydoni kiritiladi.
- "s" \(-\) Qulmamatni;
- "x" \(-\) poyizdning bir bo'lagini;
- Nuqta bo'sh maydonni ifodalaydi.
Chiqish faylida har bir test uchun alohida satrlarda Qulmamat tunnelning nargi tarafiga o'ta olsa "yes", aks holda "no" so'zini chop eting.
Poyizd o'chami doim \((1\times j)\) \((2\leq j\leq m)\) ko'rinishida bo'ladi. Qulmamat doim bo'sh maydonga yuraoladi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 3 10 s.xx...... .....xxxxx .xxxxxx... 3 10 s.xx...... ....xxxxxx .xxxxxx... |
yes no |
C. Ketma - ketlik #1
Xotira: 16 MB, Vaqt: 500 msSizga misol ko'rinishida ketma - ketlik beriladi siz bu ketma - ketlik javobini chiqarishingiz kerak bo'ladi. Agar ketma - ketlik uzun bo'lsa boshlang'ich va so'nggi hadlari sizga beriladi va oraliq nuqtalar bilan to'ldiriladi. Ketma - ketlik doim 1 dan boshlanadi.
Yagona qatorda sizga ketma - ketlik misoli beriladi. Ketma - ketmalikda sonlar \(10^{36}\) dan oshmasligi kafolatlanadi.
Masala javobini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1-4 |
-3 |
| 2 |
1-4+9-....+9801-10000+10201 |
5151 |
D. Mr. Quloq
Xotira: 5 MB, Vaqt: 250 msShohruh Mirzo o'rtoqlari bilan hazillashishni yaxshi ko'radi. Bu safar u ortoqlari nima desa ham o'zlarining gapini qaytarib turaverishni o'ylab topdi.
Sizga o'rtoqlaridan birining Shohruh Mirzoga aytgan gapi beriladi
Siz Shohruh Mirzo nima deyishini chiqarishingiz kerak.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
Bu example emas! |
Bu example emas! |
E. Tanish masala
Xotira: 16 MB, Vaqt: 1000 msJahongir matematika kitobida bir mantiqiy masalaga ko'zi tushib qoldi. Ushbu masala ko'pchilikka tanish bo'lsa kerak. Mana o'sha masala : raqamlari yig'indisi \(2006\) ga teng bo'lgan sonni ikkita teng natural sonlar ko'paytmasi ko'rinishida tasvirlash mumkinmi? Jahongir bu masalani mantig'ini topdi. Endi u ixtiyoriy natural son uchun bu bajariladimi yo'qmi tekshirib bilmoqchi. Jahongirning baxtiga dasturchilikdan ozgina xabari bor. Shuning uchun u bu masala uchun dastur tuzishga qaror qildi. Ushbu dasturni Jahongirdan oldin tuzishga harakat qiling.
Biror sonning raqamlari yig'indisi \(n(n\le 10^{18})\) natural son kiritiladi.
Agar raqamlari yig'indisi \(n\) ga teng bo'lgan biror kvadrat son mavjud bo'lsa Ha, aks holda Yo'q degan yozuvni chop eting.
1 - testda : \(7 = 2+5\) ya'ni \(25\) ning raqamlari yig'indisi shaklida ifodalash mumkin.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
7 |
Ha |
| 2 |
2006 |
Yo'q |
F. AB, BA
Xotira: 24 MB, Vaqt: 1000 msSizga s satr berilgan. Satrni ichida "AB" , "BA" qism satrlar bo'lishi kerakki ular bir-biri bilan kesishmagan bo'lsin.
Masalan: "ABA" bunda "AB" qism satr ham bor , "BA" qism satr ham bor lekin ular bir-biri bilan kesishgan. "ABVBA" esa yuqoridagi shartlarni bajaradi.
Agar s satr berilgan shartlarni bajarsa "YES" aks holda "NO".
Bir qatorda \(s(1 \le |s| \le 10^5)\) satr.
Bir qatorda masala javobi "YES" yoki "NO".
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
ABA |
NO |
G. Ko'paytmalar ketma - ketligi
Xotira: 16 MB, Vaqt: 1000 ms\(2,3,10,21,55,104,\dots\) ketma-ketlik berilgan. Ketma - ketlikning \(n\) - hadini toping.
Bitta butun son \(n(1\le n \le 20)\) kiritiladi
Ketma - ketlikning \(n\) - hadini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 |
2 |
H. GAME
Xotira: 2 MB, Vaqt: 500 msAzimjon va Azizbek ko'p birgalikda o'yin o'ynashadi. Ular har doim bir xil o'yin o'ynashdan zerikkanlari bois Politsiyachi va Qochoq o'yinini o'ynamoqchi bo'lishdi. Siz ularga yordam bering. Ular NxN jadvalda P va Q harflarini joylashtirib chiqadi bunda P-politsiyachi degani Q-Qochoq degani
- jadvaldagi har bir katakchada P yoki Q harfi bor.
- Politsiyachi o'g'rini qo'lga olishi uchun o'g'ri ham politsiyachi ham bitta qatorda bo'lishi shart va bitta politsiyachi faqat bitta qochoqni tuta oladi.
- Politsiyachi o'zidan uzog'i bilan K masofa uzoqdagi qochoqni tuta oladi.
Siz ushbu o'yinda politsiyachi uzog'i bilan nechta qochoqni tutishi mumkinligini toping.
Manba: MyContest.uz
- Birinchi qatorda \(t(0 < t < 101)\) testlar soni.
- Ikkinchi qatorda \(N(2 < N < 1000) K(0 < K < N)\) sonlari o'z navbatida Jadval o'lchami va politsiyachi borishi mumkin bo'lgan masofa.
- Keyingi N ta qator va N ta ustun da probel bilan ajratilgan 'P' va 'Q' harflari mavjud.
Har bir sinov ishi uchun jadval ichida ushlanishi mumkin bo'lgan o'g'rilarning maksimal sonini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 3 1 P Q P Q P Q Q Q P |
3 |
I. Degree Game
Xotira: 16 MB, Vaqt: 1000 msAzimjon va Sardor "Degree Game" o'yini boshlab yuborishdi. O'yinda bitta natural N soni tanlab olinadi va 1 dan N sonigacha bo'lgan natural sonli qator hosil qilinadi.
O'yin boshlangandan keyin esa Azimjon 1 dan N gacha bo'lgan ixtiyoriy X natural sonni tanlaydi. Keyingi qadamda esa sonli qatordan X ning barcha natural darajalari chiqarib yuboriladi (x1,x2,x3,....). Keyin esa huddi shu ishni Sardor ham takrorlaydi.
O'yin mobaynida kimning navbatida tanlash uchun son qolmasa o'sha ishtirokchi yutqazgan hisoblanadi.
Azimjon ham Sardor ham bu o'yinni juda yaxshi bilishadi va ikkalasi ham optimal o'yinchilar deb hisoblansin.
Bitta qatorda N natural soni. (1 ≤ n ≤ 109)
O'yin g'olibi ("Azimjon" yoki "Sardor") ismini chiqaring.
1-testda sonli qatorda faqat 1 soni bor va uni Azimjon tanlaydi. Sardorga esa son qolmaydi va Azimjon g'olib bo'ladi.
2-testda esa sonli qatorda faqat 1 va 2 sonlari bor Azimjon ixtiyoriy birini tanlagan taqdirda ham Sardor uchun bitta son qoladi va Azimjonning navbatdagi urunishiga son qolmaydi, shu sababli Sardor g'olib bo'ladi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 |
Azimjon |
| 2 |
2 |
Sardor |
| 3 |
8 |
Sardor |
J. Myobius funksiya
Xotira: 16 MB, Vaqt: 1000 msSizga \(n\) soni beriladi. \(n\) ni tub ko'paytuvchilarga ajratganda \(n=p_1^{α_1}*p_2^{α_2}*p_3^{α_3}*......p_k^{α_k}\) bo'lsa, \(M(n)\) ni chop eting.
\(M(n) = 1 , n=1\).
\(M(n) = 0 , ∃ α_i > 1 ,1 \le i \le k\).
\(M(n) = (-1)^k , α_i=1 , 1 \le i \le k\).
Bitta butun son \(1 \le n \le 10^5\) kiritiladi.
Masala javobini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
81113 |
1 |
K. Other gcd
Xotira: 16 MB, Vaqt: 1000 msSizga \(a,n,m\) sonlari beriladi. Siz \(a^n-1\) va \(a^m-1\) ning ekubini ekranga chiqazishingiz lozim.
Bir qatorda \(a,n,m\) \(1 \le a,n,m \le 10^{18}\) sonlari kiritiladi.
Masala javobini \(10^9+7\)ga bo'lgandagi qoldig'ini chop eting
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 3 5 |
1 |
L. Shakl
Xotira: 16 MB, Vaqt: 1000 ms\(N\) ta nuqtadan tashkil topgan va bu nuqtalardan kamida \(2\)ta kesma chiqgan shakl bor. Sizga shu shaklning barcha nuqtalaridan chiqgan kesmalar soni beriladi. Siz shu shaklni qo'l uzmasdan va bir kesmadan ikki marta yurmasdan barcha kesmadan o'tib bo'ladimi yoki yo'qmi aniqlashingiz kerak.
Kirish faylining birinchi satrida \(N\) (\(3 \le N \le 1000\)) soni kirtiladi.
Keyingi qatorda \(N\)ta \(N-1\) dan oshmagan natural son kiritiladi.
Agar bu shaklni qo'l uzmasdan chizib bo'lsa “Yes”, aks holda “No” so’zlarini chiqaring.
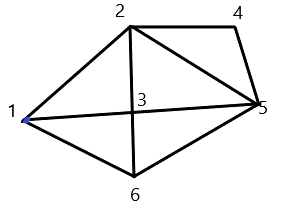
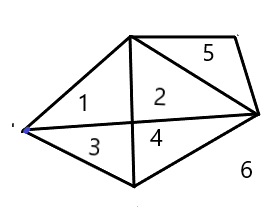
\(1)\) Birinchi rasmda 1-nuqtadan 3ta, 2-dan 4ta, 3-dan 4ta, 4-dan 2ta, 5-dan 4ta va 6-dan 3ta kesma chiqgan.
\(2)\) Ikkinchi rasm ham birinchi bilan bir xil lekin unda o'rtagi nuqta dioganal kesishish nuqtasi hisobida olinmoqda. Bu rasmda 1-nuqtadan 3ta, 2-dan 4ta, 3-dan 2ta, 4-dan 4ta va 5-dan 3ta kesma chiqgan.
Bu ikkala shaklni ham qo'l uzmasdan chizish mumkin.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 3 4 4 2 4 3 |
Yes |
M. Qiziqarli funksiya
Xotira: 16 MB, Vaqt: 1000 msSIzga \(n\) soni beriladi . Bu sonni tub ko'paytuvchilarga ajratilgan holati \(n = p_1^{α_1}*p_2^{α_2}*p_3^{α_3}*.....*p_k^{α_k}\).
\(f(x)=x^2\).
\((1+f(p_1)+f(p_1^{2})+f(p_1^{3})+...+f(p_1^{α_1}))*(1+f(p_2)+f(p_2^{2})+f(p_2^{3})+...+f(p_2^{α_2}))*....*(1+f(p_k)+f(p_k^{2})+f(p_k^{3})+...+f(p_k^{α_k}))\)
ni toping.
Birinchi qatorda n soni kiritiladi \(1 \le n \le 10^{6}\).
Masala javobini 1000000007 bo'lgandagi qoldiqni chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5062 |
32029810 |
N. Bo'laklashlar 2
Xotira: 16 MB, Vaqt: 1000 msDilshod kombinatorikani uncha yaxshi bilmas ekan. U sizdan ushbu misolni yechishga yordam so'radi. Unga yordam bering. \(n+1\) ta elementli \(A\) to’plamdan aynan \(2\) ta bo’laklashlar soni nechta? Masalan: \(A=[1,2,3,4]\) bo’lsa uning bo’laklashlari\([1] [2,3,4] , [2] [1,3,4] , [3] [2,1,4] , [4] [2,3,1] , [1,2] [3,4] , [1,3] [2,4] , [1,4] [2,3]\) – \(7\) ta.
Kirish faylining birinchi satrida bitta natural son \((2 \le n \le 10^{18})\) beriladi
Masala javobini \(1000000007\)ga bo'lgandagi qoldiqni chop eting
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 |
7 |
O. Bo'laklashlar 3
Xotira: 16 MB, Vaqt: 1000 msDilshod kambinatorikani uncha yaxshi bilmas ekan . U sizdan yana bir misolni yechishga yordam so'radi . Unga yordam bering.\(n+1\) ta elementli \(A\) to’plamdan aynan 3 ta bo’laklashlar soni nechta? Masalan: \(A=[1,2,3,4]\) bo’lsa uning bo’laklashlari \([1] [3] [2,4] , [3] [2] [1,4] , [1] [4] [3,2] , [4] [2] [3,1] , [1] [2] [3,4] , [3] [4] [1,2]\) – 6 ta
Kirish faylining birinchi satrida bitta natural son \(3 \le n \le 10^{18}\) beriladi.
Masala javobi juda katta bo’lishi mumkin, shuning uchun uni \(10^9 + 7\) ga bo’lgandagi qoldiqni chop eting
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 |
6 |
| 2 |
4 |
25 |
P. Matritsa: Qayta yuklanish
Xotira: 16 MB, Vaqt: 1000 msNeo matritsani mo'jizaviy deb hisoblaydi, agar u quyidagi talablarga javob bersa:
- \(N × N\) o'lchamlarga ega.
- Uning barcha elementlari \(1\) dan \(2×N-1\) gacha bo‘lgan butun sonlardir.
- \(N - 2\) ning darajasi (ya'ni, \(2K = N\) bo'lgan manfiy bo'lmagan butun K soni mavjud).
- Har bir \(i\) soni \((1 ≤ i ≤ N)\) uchun i-qator va i-ustunning barcha elementlari \(1\) dan \(2×N-1\) gacha boʻlgan barcha raqamlarni oʻz ichiga olgan toʻplamni tashkil qiladi.
Agent Smit yaqinda Neo-ga har qanday manfiy bo'lmagan butun \(K\) uchun ajoyib \(2K × 2K\) matritsani qurish mumkinligini aytdi. Neo Agent Smitga ishondi va endi 1 dan 9 gacha bo'lgan har bir \(K\) uchun kamida bitta mo''jizaviy matritsa topmoqchi. U yana bir bor yordam so'rab sizga murojaat qiladi.
Neo sizdan \(K\) raqami berilganda ajoyib \(2K × 2K\) matritsani topadigan dastur yozishingizni xohlaydi.
INPUT.TXT kiritish fayli bitta butun K(0≤K≤9) dan iborat son.
OUTPUT.TXT chiqish faylida \(2K×2K\) o'lchamdagi ajoyib matritsa chiqadi. Agar bunday matritsalar bir nechta bo'lsa, istalgan birini chop etishga ruxsat beriladi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 |
1 3 2 1 |
| 2 |
2 |
1 3 6 7 2 1 7 6 4 5 1 3 5 4 2 1 |