A. To’plam osti
Xotira: 16 MB, Vaqt: 1000 msN ta elementdan iborat to’plam berilgan. Sizning vazifangiz shu to’plamdan maksimum sondagi elementlarni shunday ajratib olishki, olingan elementlar ichida ixtiyoriy har xil ikkitasi tanlanganda yig’indi hech qachon K ga bo’linmasin.
INPUT.TXT kirish faylining dastlabki satrida ikkita butun son, N(1 ≤ N ≤ 105) va K(1 ≤ K ≤ 100), keyingi satrda N ta [1, 109] oralig’idagi butun sonlar, to’plam elementlari kiritiladi.
OUTPUT.TXT chiqish faylida yagona son, masala shartiga muvofiq maksimum nechta element ajratib olinishi mumkinligini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 3 1 7 2 4 |
3 |
| 2 |
5 5 2 7 12 17 22 |
5 |
B. 0 va 1 lar soni
Xotira: 16 MB, Vaqt: 1000 msAziz juda katta B binar soni ustida ishlamoqda. Son juda katta bo’lganligi bois sizga bu son A butun sonli massivga ixchamlashtirilgan holatda beriladi, ixchamlashtirishda ketma-ketligi mos ravishda (A0, A2, A4, …) juft indekslarda navbati kelgan 1 lar soni, (A1, A3, A5, …) toq indekslarda navbati kelgan 0 lar soni saqlanadi. Aziz jami 0 lar soni va jami 1 lar soni B sonikiga teng bo’lgan, eng kichik C(>B) binar sonini hosil qildi. Siz Aziz hosil qilgan C sonining ixchamlashtirilgan shaklini D massivni hosil qiling.
INPUT.TXT kirish faylining dastlabki satrida bitta butun son, T(1 ≤ T ≤ 100) testlar soni kiritiladi.
Keyin har bir test uchun alohida ikkita qatorda ma’lumotlar quyidagicha kiritiladi:
- Birinchi qatorda bitta butun N(1 ≤ N ≤ 10) soni, A massiv uzunligi
- Ikkinchi qatorda N ta butun son, A massiv elementlari. (1 ≤ Ai ≤ 1018)
OUTPUT.TXT chiqish faylida har bir test uchun alohida ikkita qatorda quyidagi shaklda javobni chop eting:
- Birinchi qatorda bitta butun M soni, D massiv uzunligi
- Ikkinchi qatorda M ta butun son, D massiv elementlarini bo’sh joy bilan ajratilgan holda chop eting, (1 ≤ Di)
Har bir test uchun mos keluvchi javob borligi kafolotlanadi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 5 4 1 3 2 4 |
7 4 1 3 1 1 1 3 |
C. Qism satr
Xotira: 16 MB, Vaqt: 1000 msUzungligi \(N\) bo`lgan \(S\) satr beriladi, berilgan satrdan shunday eng uzun qism satrni topingki unda bir xil harf ko`pi bilan \(K\) marta qatnashgan bo`lsin.
Masalan:
\(N = 6, K = 1\)
\(S = “Husayn”\)bunda javob sifatida \(“Husayn”\) olinsa bo`ladi, chunki hamma harf bir martadan qatnashgan.
Ammo:
\(N = 7, K = 1 \newline S = “Hasanov”\)
bunda esa \(“Has”\) yoki \(“sanov”\) ni olish mumkin xolos shart bo`yicha eng uzuni “sanov” olinadi.
Bunday satrlar juda ham ko`p bo`lishi mumkin, sizning vazifangiz satrning uzunligi topish.
Birinchi qatorda \(N\) va \(K (1 \le K \le N \le 10^5)\) butun sonlari mos ravishda satr uzunligi va qism satr uzunligi.
Keyingi qatorda \(N\) uzunlikga ega lotin harflaridan iborat \(S\) satr beriladi
Yagona butun son, shartni qanoatlantirishi mumkin bo`lgan qism satr uzunligini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 1 Husayn |
6 |
| 2 |
7 1 Hasanov |
5 |
D. Ajoyib sonlar
Xotira: 16 MB, Vaqt: 1000 msNatural bo’luvchilar soni toq bo’lgan sonlar ajoyib sonlar deyiladi. Berilgan N soni ajoyib son yoki yo’qligini aniqlang.
Kirish faylining dastlabki satrida bitta butun son, T (1 ≤ T ≤ 1000) testlar soni kiritiladi. Ikkinchi satrdan boshlab har bir test uchun alohida satrda bitta butun son N (1 ≤ N ≤ 1018) soni kiritiladi.
Chiqish faylida har bir test uchun alohida qatorda agar N soni ajoyib son bo’lsa YES aks holda NO so’zini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 1 3 7 169 |
YES NO NO YES |
E. Nisbat 2
Xotira: 16 MB, Vaqt: 1000 msQuyidagi formulani hisoblang:
\(\cfrac{a + a^2+a^3+\dots+a^n}{a^{-1}+a^{-2}+\dots+a^{-n}}\)
INPUT.TXT kirish faylining birinchi satrida ikkita natural son \(a \le 10^9, n \le 1000\) beriladi
Masala javobini \(10^9+7\) ga bo'lgandagi qoldiqni chop eting
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 2 |
8 |
F. Rangli markerlar
Xotira: 16 MB, Vaqt: 1000 msSizga kvadrat katakchalardan iborat cheksiz jadval beriladi. Dastlab, barcha katak oq rangda.
Sizda qizil va ko'k marker bor. Siz jami a ta katakni qizil marker bilan, b ta katakni ko’k marker bilan bo'yashingiz mumkin. Bitta katakni bir vaqtda har ikkala rangda bo’yash mumkin emas. Ikkala markerni ham to’liq ishlatishingiz kerak, buning uchun jadvalda jami a ta katak qizil rangda, b ta katak ko’k rangda bo’lishi kerak.
Siz jadvalni quyidagi qonuniyat asosida bo’yashingiz kerak:
- Jadvalda yuzasi a + b ga teng bo’lgan, bo’yalgan to’rtburchak hosil bo’lishi kerak;
- kamida bitta rangdagi barcha kataklar ham to'rtburchak hosil qilsin .
To'g'ri bo’yashga ba'zi misollari:
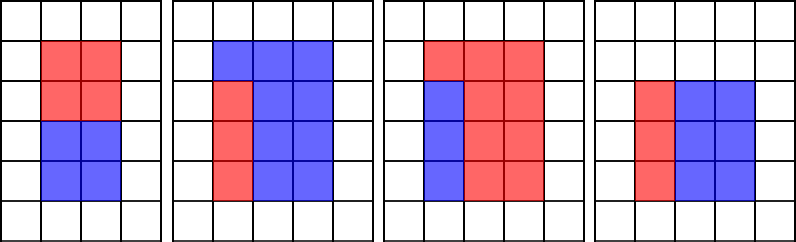
Noto’g’ri bo’yashga ba’zi misollar:
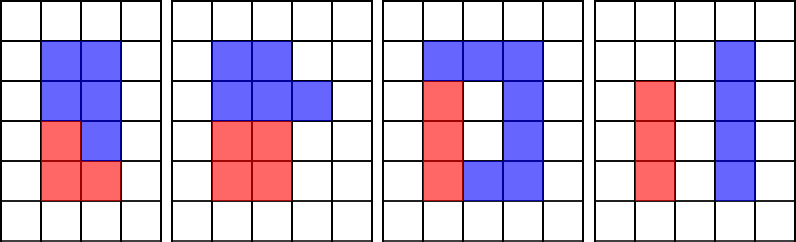
Berilgan a va b dan foydalanib to’g’ri bo’yash hisoblanadigan to’rtburchaklar ichidan perimetri eng kichik bo’lgan to’rtburchakning perimetrini aniqlang.
Kirish faylining yagona satrida ikkita butun son, \(a\) va \(b(1 \le a,b \le 10^{14})\), qizil va ko’k markerda bo’yalishi kerak bo’lgan kataklar soni kiritiladi.
Chiqish faylida yagona butun son, masala yechimini chop eting!
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 4 |
12 |
| 2 |
3 9 |
14 |
| 3 |
9 3 |
14 |
| 4 |
3 6 |
12 |
G. Fibonacci - qoldiq
Xotira: 16 MB, Vaqt: 1000 ms\(F(0)=0 , F(1)=1 , \space \dots \space, F(n) = F(n-1) + F(n-2) ( n > 1 )\) ketma-ketlik Fibonacci ketma-ketligi deyiladi. Sizni vazifanggiz \(i\) - fibonacci sonini \(j\) - fibonacci soniga bo'linishini tekshirish.
Dastlabki qatorda \(T ( T ≤ 10 )\) testlar soni kiritiladi. Keyingi qatorda har bir test uchun 2 tadan butun son \(i\) va \(j\) sonlari kiritiladi \(( 1 ≤ i , j ≤ 10^{18} )\)
Chiqish faylida har bir test uchun alohida \(F(i) \space F(j)\) ga qoldiqsiz bo'linsa YES aks holda NO so'zi chop etilsin
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 5 3 |
NO |
H. Murakkab tenglama
Xotira: 16 MB, Vaqt: 1000 ms\(ax^3+bx^2+cx+d=0\) ko'rinishidagi tenglama berilgan bo'lsin. Biz 3-darajali tenglamani kamida bitta butun ildizga ega bo'lgan paytida Murakkab tenglama deb atashimiz mumkin.Sizga \(a,b,c,d\) sonlar berilgan bo'lsa \((a ≠ 0)\), ushbu matematik ifoda Murakkab tenglama bo'la oladimi yoki yo'qligini aniqlashdan iborat.
Kirish faylining yagona satrida \(4\) ta butun sonlar \((-10^{12} ≤ a,b,c,d ≤ 10^{12})\) kiritiladi.
Chiqish faylida agar tenglama "Murakkab tenglama" bo'lsa "Yes", aks holda "No" so'zini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 2 3 2 |
Yes |
| 2 |
1 0 0 0 |
Yes |
I. Rangli kataklar.
Xotira: 24 MB, Vaqt: 1000 msMironshoh \(N*N\) to'rga va qizil bo'yoqga ega. U to'r chiroyli bo'lishi uchun \((i,j)\) katakni bo'yashi kerak agar \(i+j\) tub bo'lsa \((0 \le i,j \le n-1)\). U shunaqa tartibda kataklarni bo'yab chiqdi.
U bo'yagandan keyin nechta rangli kataklar bo'lganini topish.
Bir qatorda \(N(1 \le N \le 1000000)\) soni.
Bo'yalgan kataklar sonini \(10^9+7\) ga bo'lgandagi qoldiq.
n=3 bo'lganda
0-bo'sh kataklar 1-bo'yalgan kataklar.
000 001
000 011
000 110
\((0,2) (1,1) (1,2) (2,0) (2,1)\) shu kataklar bo'yaladi chunki i+j larni yig'indisi tub.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 |
0 |
| 2 |
2 |
1 |
J. Uy ishi
Xotira: 16 MB, Vaqt: 1000 msQuvonchbek matematkani yaxshi bilganligi uchun ustozi unga "expression module" ga oid bo'lgan misol berdi. Misol quydagicha edi:
- \((1^n+2^n+3^n+4^n) \space mod \space5\)
Quydagi ifodani natijasini olishda Quvonchbekga yordam bering.
Yagona qatorda n(\(0\leq n \leq 10^{10^5}\) butun son kiritiladi.
Masala javobini chop eting.
- \((1^4+2^4+3^4+4^4) \space \text{mod} \space 5 \text{=}(1+16+81+256) \space \text{mod}\space =354 \space \text{mod} \space 5 = 4\)
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 |
4 |