A. Qiziqarli taqqoslash
Xotira: 32 MB, Vaqt: 2000 msAzimjon doskaga ikkita son yozdi. Ikkalasi ham quyidagi formatda berilgan: \(x\) musbat son va \(p\) oxirdan qo'shish kerak bo'lgan nollar soni.
Endi sizdan Azimjon bu ikki sondi solishtirishingizni so'radi. Unga yordam bera olasizmi?
Kirish faylining dastlabki satrida \(x_1, p_1(1\leq x_1 \leq 10^6, 0\leq p_1\leq 10^6)\) birinchi sondi tavsifi. Ikkinchi satrda \(x_2, p_2(1\leq x_2 \leq 10^6, 0\leq p_2\leq 10^6)\) ikkinchi sondi tavsifi beriladi.
Chiqish faylida agar birinchi son katta bo'lsa ‘>’, agar ikkinchi son katta bo'lsa ‘<’, agar ikki son teng bo'lsa ‘=’ belgisini chop eting.
Birinchi misolda birinchi sondi oxiridan bitta nol qo'shiladi, ikkinchi sondi oxiridan nolta nol qo'shiladi taqqoslash 20 > 19.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 1 19 0 |
> |
| 2 |
1999 0 2 3 |
< |
B. Azimjon va ketma-ketlik yig'indisi
Xotira: 32 MB, Vaqt: 2000 msAzimjonda \(3\) ta musbat butun sonlar \(a_1, a_2, a_3\) massiv mavjud. U ushbu massivning barcha ketma-ketliklari yig'indisini hisoblab chiqdi, ular kamaymaslik bo'yicha saralandi va \(b_1,b_2,...,b_7\) massivni hosil qildi.
Masalan, agar \(a=[1,4,3]\) sonlar mavjud bo'lsa, 1, 4, 3, 1+4=5, 1+3=4, 4+3=7, 1+4+3=8 yig'indilardan so'ng, saralangan \(b=[1,3,4,4,5,7,8]\) massiv hosil qilinadi.
Afsuski Azimjon dastlabki \(a\) massivini yo'qotib qo'ydi, \(b\) massivdan foydalangan holda Azimjonga o'zining dastlabki massivini tiklashda yordam bering.
Kirish faylida \(7\) ta \(b_i(1\leq b_i\leq 10^9)\) butun sonlar bitta satrda beriladi, Azimjon hosil qilgan yangi massiv.
Chiqish faylida Azimjonning dastlabki massivini chop eting bitta satrda, agar yechimlar bir nechta bo'lsa istalganini, istalgan tartibda chop etishingiz mumkin.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 3 4 4 5 7 8 |
1 4 3 |
| 2 |
1 2 3 4 5 6 7 |
4 1 2 |
C. Turli xil butun sonlar
Xotira: 32 MB, Vaqt: 2000 msSizga \(n\) ta butun sonlar qatori beriladi \(a_1, a_2, ..., a_n\). Siz ushbu sonlarning kichik to'plamini tanlashingiz mumkin(ehtimol hech birini yoki hammasini) va ularning ishorasini o'zgartirishingiz mumkin(ya'ni o'zgartirish \(x\rightarrow -x\)). Bunday operatsiyadan kiyin eng ko'p turli xil sonlar qancha bo'lishi mumkin?
Kirish faylining dastlabki satrida \(n(1\leq n\leq 10^5)\) butun soni va kiyingi satrda \(n\) ta butun son \(a_1,a_2,...,a_n(-10000\leq a_i\leq 10000)\) massiv elementlari beriladi.
Chiqish faylida jami bo'lib nechta turli xil son hosil qilish mumkin ekanligini chop eting.
Birinchi misolda massivning birinchi va oxirgi elementining ishorasini o'zgartirishingiz mumkin \([-1, 1, 2, -2]\).
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 1 1 2 2 |
4 |
D. Ro'xlarning joylashuvi
Xotira: 32 MB, Vaqt: 2000 msSizda \(n\times n\) o'lchamli shaxmat doskasi va \(k\) ta ro'x mavjud. Sizning vazifangiz ro'xlarni shaxmat doskasiga quyidagi ikki shart asosida joylashtirishdan iborat:
- Istalgan ikki ro'x bir birga hujim holatda bo'lmasligi kerak;
- Istalgan ro'xni qo'shni \(8\) ta katakchaning biriga ko'chirganda ikki ro'x bir biriga hujim holatiga tushmasligi kerak.
Ikki ro'x hujim holatiga tushadi, agar ular joylashgan koordinatalarining \(x_1=x_2\) yoki \(y_1=y_2\) shart bajarilib qolsa.
Kirish faylida \(n,k(1\leq k\leq n\leq 40)\) butun sonlari mos ravishda shaxmat o'lchami va ro'xlar soni beriladi.
Chiqish faylida yuqorida aytilgan shartga mos holda \(k\) ta ro'xni joylashtirishning iloji bo'lsa shaxmat doskasidagi joylashuvni chop eting(yechimlar bir nechta bo'lsa istalganini). Agar yechim mavjud bo'lmasa \(-1\) ni chop eting.
Bo'sh katakchalar \('.'\) bilan, ro'xlar \('R'\) belgisi bilan tasvirlang.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 2 |
..... R.... ..... ....R ..... |
| 2 |
3 3 |
-1 |
E. Aylana stol
Xotira: 32 MB, Vaqt: 2000 msAylana stol atrofida \(N\) ta do’st o’tirishibdi. Do’stlar \(1\) dan \(N\) gacha sonlar bilan raqamlab chiqilgan. Ular judaham zerikishdi shuning uchun bir qiziqarli o’yin o’ylab topishdi. O’yin sharti quyidagicha edi:
- 1-raqamli o’yinchidan boshlab ketma-ket sanashni boshlashadi;
- Agar o’yinchi \(K\) ga karrali sonni aytsa o’yinni tark etadi;
- O’yinni tark etgan o’yinchidan so’ng sanash navbati kiyingi o’yinchiga o’tadi;
- Sanash navbati oxirgi o’yinchiga kelsa kiyingi navbat yana boshiga ko’chiriladi.
Ushbu o’yin toki 1 kishi qolgunga qadar davom etadi. Sizning vazifangiz yakunda stol atrofida qolishi kerak bo’lgan o’yinchini tartib raqamini chop etishdan iborat.
Kirish faylining yagona satrida \(N,K(1\leq N,K\leq1000)\) butun sonlari beriladi.
Chiqish faylida o'yin yakunida stol atrofida qolishi kerak bo'lgan o'yinchining tartib raqamini chop eting.
1-test:
Do'stlar 1 dan 4 gacha raqamlar bilan raqamlab chiqiladi [1, 2, 3, 4]. O'yinchilardan 2 ga karrali sonlarni aytganlar navbat bilan o'yinni tark etishi quyidagicha [1, 3, 4] → [1, 3] → [1]. Yakunda stol atrofida 1 raqamli o'yinchi qoladi.
2-test:
Do'stlar 1 dan 5 gacha raqamlar bilan raqamlab chiqiladi [1, 2, 3, 4, 5]. O'yinchilardan 3 ga karrali sonlarni aytganlar navbat bilan o'yinni tark etishi quyidagicha [1, 2, 4, 5] → [2, 4, 5] → [2, 4] → [4]. Yakunda stol atrofida 4 raqamli o'yinchi qoladi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 2 |
1 |
| 2 |
5 3 |
4 |
F. Arqonlar
Xotira: 32 MB, Vaqt: 2000 msAzimjonda \(N\) ta arqon bor, bu arqonlar uzunligi mos ravishda \(S_1,S_2,...,S_n\) ga teng. Azimjonning dadasi bu arqonlardan uzunligi maksimal bo’ladigan bir xil \(K\) ta arqon kesib olishini aytdi.
Azimjon bu ishni uddalay olmaganligi sababli sizdan yordam so’rashga qaror qildi. Ushbu masalani yechishda Azimjonga dastur tuzib bering.
Kirish faylining dastlabki satrida \(N(1\leq N\leq 10^4)\) butun son, Azimjondagi arqonlar soni. Kiyingi satrda \(N\) ta butun son \(S_1,S_2,...,S_n\) arqon uzunliklari, uzunlik \(10^7\) dan oshmaydigan musbat butun son. Kiyingi satrda \(K(1\leq K\leq 10^4)\) butun soni beriladi.
Chiqish faylida Azimjon qirqib olishi mumkin bo'lgan \(K\) ta bir xil maksimal uzunlikka ega bo'lgan arqon uzunligini \(eps=10^{-6}\) aniqlikda chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 802 743 457 539 11 |
200.500000 |
| 2 |
4 16 8 6 11 7 |
5.333333 |
G. Azimjon va daraxt
Xotira: 32 MB, Vaqt: 2000 msAzimjon daraxtlar dunyosiga chuqurroq nazar solishga qaror qildi. U tabiatni matematika tili orqali tushunmoqchi edi.
Faraz qiling, Azimjon daraxtni graf sifatida ifodalaydi: bu grafda
- uchlar (tugunlar) — daraxtning shoxlari,
- qirralar esa — ularni bog‘lovchi yo‘llardir.
Agar daraxtda \(n\) ta uch bo‘lsa, u holda qirralar soni \(n-1\) bo‘lishi aniq — chunki bu graf daraxt (ya’ni, ulanma va siklsiz).
Endi Azimjon shunday savol ustida bosh qotirmoqda:
Daraxtdagi shunday ikkita uchi topilsinki, ular orasidagi eng katta masofa mavjud bo‘lsin.
Kirish faylining dastlabki satrida \(n(2\leq n\leq 10^5)\) butun soni, daraxt uchlari soni. Kiyingi \(n-1\) ta satrda \(u_i,v_i(1\leq u_i, v_i\leq n;u_i\neq v_i)\) juftliklar, ikki uch o'rtasida qirra mavjudligini ifodalaydi. Berilgan ma'lumotlarda daraxt berilishi kafolatlanadi.
Chiqish faylida daraxtning shunday ikki uchini chop etingki, ushbu uchlar o'rtasidagi masofada maksimal sondagi qirralar mavjud bo'lsin. Javoblar bir nechta bo'lsa istalgan javobni chop etishingiz mumkin, istalgan tartibda \((u,v)\) yoki \((v, u)\) ko'rinishida.
Birinchi testda bir nechta javoblar mavjud \((2,3)\), \((3, 2)\), \((3, 4)\) va \((4,3)\)
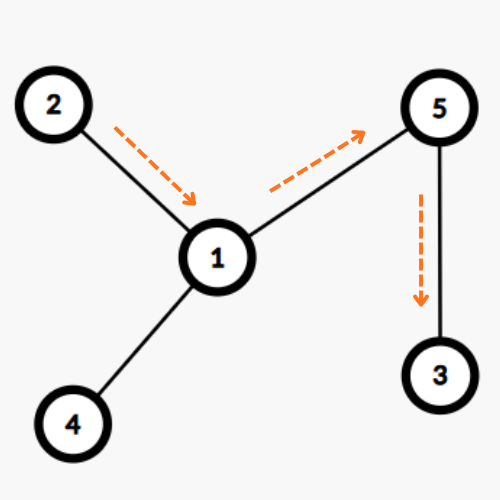
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 1 2 1 4 1 5 5 3 |
2 3 |