A. Antiqa o'rindagi tub sonlar
Xotira: 16 MB, Vaqt: 1000 ms𝐀𝐧𝐭𝐢𝐪𝐚 𝐨'𝐫𝐢𝐧𝐝𝐚𝐠𝐢 𝐭𝐮𝐛 𝐬𝐨𝐧𝐥𝐚𝐫 𝐤𝐞𝐭𝐦𝐚-𝐤𝐞𝐭𝐥𝐢𝐠𝐢 deb birinchi hadi 2 ga va keyingi har bir hadi undan avvalgi son o'rnidagi tub sonlar bo'lgan ketma-ketligiga aytiladi.
Ya'ni 2 soni birinchi tub son, keyingi had ikkinchi tub son bo'ladi. 3 soni ikkinchi tub son, keyingi hadi uchinchi tub son bo'ladi. 5 soni uchinchi tub son, keyingi had beshinchi tub son bo'ladi.
Yagona qatorda \(n\) butun soni. \(n<11\)
Ketma-ketlikdagi \(n\) - o'rinda turgan sonni chop eting
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 |
2 |
| 2 |
2 |
3 |
| 3 |
3 |
5 |
| 4 |
4 |
11 |
B. Chala matematik
Xotira: 16 MB, Vaqt: 1000 msAzimjon Matematika faniga juda ham qiziqadi. Lekin u hamma narsani chala o'rganadi.
Matematika ustozi tub sonlar haqida tushuntirganda Azimjon natural sonning 2 ta (kamida) natural bo'luvchisi topilsa u tub bo'ladi deb tushungan ekan.
Yagona qatorda moduli 1000 dan oshmaydigan butun son kiritiladi.
Azimjonning fikriga ko'ra bu "tub" yoki "murakkab" ekanligini topishingiz kerak.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 |
murakkab |
| 2 |
2 |
tub |
C. Raqamgacha raqamlari yig'indisi
Xotira: 16 MB, Vaqt: 100 msSizga \(n\) soni beriladi. Siz bir xonali son (ya'ni raqam) hosil bo'lguncha natijalarning raqamlari yig'indisini hisoblab boring.
Masalan \(29\) sonini olaylik:
\(2+9=11\)
\(1+1=2\)
Birinchi satrda \(T(T\le1000)\) testlar beriladi.
Keyingi \(T\) ta satrda bittadan \(n(1\le n\le10^{18})\) butun son kiritiladi.
Har bir test uchun alohida satrda masala yechimini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 1 |
1 |
| 2 |
7 2 3 4 5 6 7 8 |
2 3 4 5 6 7 8 |
D. Ketma - ketlikni top
Xotira: 16 MB, Vaqt: 1000 msSizga quyida ketma-ketlikning dastlabki hadlari berilgan:
1030301,10404,1092727,10816....
Sizning vazifangiz ketma-ketlikning n-hadini topish.
Yagona qatorda n(n<2*106) kiritiladi.
Ketma-ketliknig n-hadini chiqarishingiz kerak.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
7 |
1225043 |
E. Juftga aylantir
Xotira: 16 MB, Vaqt: 1000 msAbduqodirda \(n\) soni bor va bu sonda ‘0’ umuman qatnashmagan. Bu son ustida u quyidagi amalni istalgancha amalga oshirishi mumkin:
- Uzunligi \(l\) bo’lgan prefiks olishi (yoki chapdagi birinchi \(l\) ta sonni olishi) va uni teskarisiga aylantirishi mumkin. Shunday qilib, eng chapdagi son \(l\) – o’rinda turgan son bilan o’rin almashadi, ikki son esa \(l-1\) – o’rinda turgan son bilan. Agar son \(n = 123456789\) va \(l=5\) bo’lsa unda sonning yangi qiymati \(543216789\) ga teng bo’ladi.
\(l\) ning qiymati har bir operatsiya uchun turlicha bo’lishi mumkin va hatto u n ga teng bo’lishi ham mumkin.
Abduqodir juft sonlarni yaxshi ko’radi. Shu sababdan ham u \(n\) sonini yuqoridagi operatsiyalarni bajargan holda juft qilmoqchi, Ammo u bu ishni iloji boricha kamroq urinishlar bilan bajarmoqchi.
Abduqodirga \(n\) sonini eng kamida nechta urinishda juft qilish mumkinligini topishda yordam bering yoki bunday qilishning iloji yo’qligini ayting.
Siz \(t\) ta so’rovga javob berishingiz kerak.
Birinchi qatorda sizga \(t\) soni beriladi. \((1 ≤ t ≤ 100000)\)
Keyingi \(t\) ta qatorning har birida sizga bitta son – n soni beriladi \((1 ≤ n < 10^9)\)
\(T\) ta qatorning har birida shu qatorga mos keladigan so’rovning qiymatini – shu sonni juft qilish uchun kerak bo’ladigan minimal urinishlar sonini chiqaring, agar buning iloji bo’lmasa \(-1\) chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 3876 387 4489 3 |
0 2 1 -1 |
F. B-daraja
Xotira: 160 MB, Vaqt: 5000 msElbekka ustozi a ning b -inchi darajasini hisoblovchi dastur tuzishni topshiriq qilib berdi. Bu son juda ham katta bo'lib ketishini hisobga olgan o'qituvchi ab ni 109+7 ga bo'lgandagi qoldig'ini topishini aytdi. Elbek bu topshiriqni ertaga topshirishi kerak, bo'lmasa ustozi unga ″shu dasturni ham tuza olmadingmi ?″ deb koyib beradi. Elbekka bu dasturni tuzishda yordam bering.
INPUT.TXT kirish faylining 1-satrida bitta butun son, N(1 ≤ N ≤ 2*105) mavjud testlar soni kiritiladi. Keyingi N ta qatorda esa mos ravishda a, b(0 ≤ a,b ≤ 109) sonlari bo'sh joy bilan kiritiladi.
OUTPUT.TXT chiqish faylida esa ab ning har bir qiymatini 109 + 7 ga bo'lgandagi qoldiqni chiqaring.
00 = 1. (1-test na'munadagidan farq qiladi.)
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 4 2 8 123 123 |
81 256 921450052 |
G. Ajoyib massiv
Xotira: 1 MB, Vaqt: 100 msSizga N butun soni berilgan.
N uzunlikdagi P massivni shunday tuzing-ki.
Barcha i (1≤i≤N−1) uchun abs(Pi+1−Pi) i ga teng bolsin.
P massiv 1 dan N gacha bolgan sonlarndan tashkil topgan bolsin!
N \((1 <= N <= 10^5)\) kiritiladi.
Massiv elementlarini bir qatorda boshliq bilan chop eting.
Hosil bolgan massiv eng kichik bo`lishi kerak!
1-test:
[2,3,1] va [2,1,3] massivlar bo`lishi mumkin lekin [2,1,3] massivni chiqarish kerak. 213<231
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 |
2 1 3 |
H. Oxirgi raqam.
Xotira: 8 MB, Vaqt: 100 msSizga N factorial beriladi berilgan N faktorialning noldan farqli oxirgi raqamini topshingiz kerak.
Birinchi qatorda n butun soni beriladi\((0\le |N| \le10^9)\).
Chiqish faylida N factorialning 0dan farqli bo'lgan oxirgi raqamini chiqaring.
Agar bunday son mavjud bo'lmasa -1 ni chiqaring.
.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 |
2 |
I. C-daraja
Xotira: 16 MB, Vaqt: 1000 msBu masala "B-daraja" masalasini qisman davomi hisoblanadi. Bu masalada siz \(a^{b^{c}}\) mod 109 + 7 ni topishingiz kerak.
INPUT.TXT kirish faylining 1-satrida bitta butun son, N(1 ≤ N ≤ 2*105) mavjud testlar soni kiritiladi. Keyingi N ta qatorda esa mos ravishda a, b, c(0 ≤ a,b,c ≤ 109) sonlari bo'sh joy bilan kiritiladi.
OUTPUT.TXT chiqish faylida esa \(a^{b^{c}}\) ning har bir qiymatini 109 + 7 ga bo'lgandagi qoldiqni chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 3 7 1 15 2 2 3 4 5 |
2187 50625 763327764 |
J. Uchta uch
Xotira: 16 MB, Vaqt: 1000 ms\(n\) ta uchga ega graf tekislikka izomorf tushirilganda 3 ta uch bilan hosil bo'lgan bo'lak(yuza) bo'lmasa,qirralar bo'lishi mumkin bo'lgan maksimal qiymatni toping.(Kesishish nuqtalari uch xisoblanmaydi!)
Birinchi qatorda \(2 kiritiladi.
Masala javobini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 |
2 |
K. Function
Xotira: 5 MB, Vaqt: 100 ms\(f : N →N\).
\(f(f(n))+f(n+1)=n+2 , \forall n \in N\).
Sizga m soni beriladi.\(f(m)\) ni toping.
Sizga birinchi qatorda \(1 soni beriladi.
Masala javobini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 |
4 |
L. Chess
Xotira: 16 MB, Vaqt: 1000 ms Ushbu masalada sizga \(8\times8\) maydonda bo'lib o'tadigan standart shaxmat o'yinining qaysidur jarayoni beriladi. Bu jarayonda yurish navbati sizga kelib qolgan va usha jarayonda faqatgina bitta yurish bilan raqibni mot qilishingiz kerak bo'ladi.
Ushbu masalada sizga \(8\times8\) maydonda bo'lib o'tadigan standart shaxmat o'yinining qaysidur jarayoni beriladi. Bu jarayonda yurish navbati sizga kelib qolgan va usha jarayonda faqatgina bitta yurish bilan raqibni mot qilishingiz kerak bo'ladi.
Misol: Agar siz oq toshlarda o'ynayotgan bo'lsangiz C5 da joylashgan ot ni D7 ga olib o'tish orqali raqibni bir marotaba yurishda mot qilish mumkun(1-test).
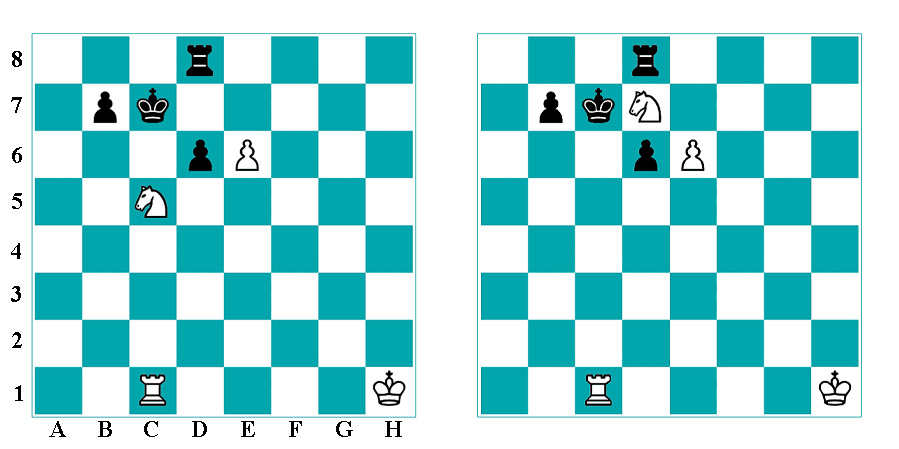
Shaxmat tosh donalari quyidagicha belgilanadi: King(shox) - K, Queen(farzin) - Q, Bishop(fil) - B, Knight(ot) - N, Rook(rux) - R va Pawn(piyoda) - P. Oq va qora toshlar mos ravishda katta kichik harflar bilan va bo'sh maydon nuqta bilan ifodalanadi.
Kirish faylining dastlabki satrida \(k(0\leq k\leq 1)\) butun son ya'ni 0 yoki 1 bu mos ravishda siz o'yinni qora yoki oq toshlarda davom ettirishingizni anglatadi. Kiyin \(8\times8\) maydonda o'yin jarayoni tasvirlanadi.
Siz shunday bir toshni boshqa maydonga kuchirish orqali shoxga hujum qilishingiz kerak natejada shox hujum ostida qolsin. Ko'chirilishi kerak bo'lgan toshning dastlabki va kiyingi koordinatasini mos ravishda probil bilan ajratilgan holda(agar bunday yechimlar bir nechta bo'lsa istalganini) chop eting. Yechim mavjudligi kafolatlanadi.
Piyoda harakati siz oq yoki qora toshlarda o'ynashingizdan qati nazar faqat bir tomonlama bo'ladi 2-testga qarang.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 ...r.... .pk..... ...pP... ..N..... ........ ........ ........ ..R....K |
C5 D7 |
| 2 |
0 ....K.R. .Pp..P.P ....Bb.. ..pP.... R.....p. .......p ....r... .......k |
C7 C8 |
M. Ariadna ipi
Xotira: 16 MB, Vaqt: 1000 msTezeyga Minotavr labirintidan to'p ip yordam berdi. To'p o'rniga shaxsiy kompyuterdan foydalanishingiz mumkin.
Vazifa labirintda Tezusning marshrutiga kiradigan dasturni yozish va Tezus labirintdan o'lik yoki halqalarsiz chiqish uchun eng qisqa yo'lni topishdir.
INPUT.TXT kiritish faylida Tezus marshruti mavjud bo'lib, u harflardan iborat qator bilan ifodalanadi: N, S, W, E va uzunligi 1 dan 200 gacha.
Harflar quyidagilarni anglatadi:
N - shimolga bir ″qadam″,
S - janubga bir ″qadam″,
W - g'arbga bir ″qadam″,
E - sharqqa bir ″qadam″.
Topilgan qaytish yo'li OUTPUT.TXT chiqish fayliga kirish fayliga o'xshash tarzda yoziladi. Agar marshrut noaniq bo'lsa, u quyidagi ustuvorlikka muvofiq tanlanishi kerak: N, E, S, W.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
EENNESWSSWE |
NWW |