A. Increment va Decrement
Xotira: 32 MB, Vaqt: 1000 msN ta butun sonlar massivi mavjud. Dastlab, har bir element 0 ga teng. Q so'rovlar mavjud bo'lib, ularning har biri quyidagilardan iborat:
- \(1\ X\ Y\): birinchi X ta elementlarning qiymatini Y ga oshiring.
- \(2\ X\ Y\): oxirgi X ta elementlarning qiymatini Y ga kamaytiring.
Barcha so'rovlarni bajargandan so'ng, har bir element o'zining mutlaq qiymati bilan almashtiriladi. Nihoyat, massivning eng katta elementining qiymati qanday?
Kirish faylining birinchi qatorida 2 ta butun son - N va Q \((1 \le N \le 10^9, 1 \le Q \le 10^5)\) kiritiladi. Keyingi Q ta qatorning har birida 3 tadan butun son - T, X, Y \((T \isin (1, 2), 1 \le X \le N, 1 \le Y \le 10^9)\) kiritiladi.
Barcha so'rovdan so'ng, massivdagi absolyut qiymati eng katta bo'lgan sonni chop eting.
Massiv eng birinchi quyidagi ko'rinishda edi: [0, 0, 0, 0, 0, 0].
Birinchi so'rovdan so'ng: [3, 3, 0, 0, 0, 0]
Ikkinchi so'rovdan so'ng: [3, 3, 0, -5, -5, -5]
Uchinchi so'rovdan so'ng: [4, 4, 1, -4, -5, -5]
Har bir elementni mutlaq qiymati bilan almashtirgandan so'ng, massiv [4, 4, 1, 4, 5, 5] bo'ladi. Massivdagi eng katta elementining qiymati 5 ga teng.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
6 3 1 2 3 2 3 5 1 4 1 |
5 |
B. Binolar
Xotira: 64 MB, Vaqt: 1000 msRobolandiyada n ta ketma-ket bino mavjud, bunda i-bino \(A_i\) qavatdan tashkil topgan. Har doimgidek Robolandiyaga yana yangi hokim saylandi va endi u ketma-ket k ta binoning qavatlari sonini bir xil qilmoqchi. Biror bino ustiga 1 ta qavat qurish yoki 1 qavatni olib tashlash qiymati 1 ga teng. Hokim minimal qiymat evaziga maksimal foyda olishni xohlaydi, ya'ni minimum xarajat yordamida ketma-ket k ta binoning balandligini 1 xil qilishi kerak. Yangi hokimning boshqa vazifalari ham ko'pligi sababli bu vazifa sizga topshirildi. Minimum xarajat qancha bo'lishini aniqlang.
Birinchi qatorda n va k sonlari kiritiladi.
Keyingi n ta qatorning har birida A massiv elementlari kiritiladi.
\(1 \le k \le n \le 10^5\)
\(1 \le A_i \le 10^6\)
Birinchi qatorda minimum xarajat qancha bo'lishini chop eting.
Keyingi n ta qatorda o'zgarishlardan so'ng har bir bino qavatlari sonini chop eting.
Agar bir nechta optimal javob mavjud bo'lsa istalganini chop etishingiz mumkin.
.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 3 3 9 2 3 1 |
2 3 9 2 2 2 |
C. Satrni tiklash
Xotira: 32 MB, Vaqt: 1000 msSizga satr berilgan. Satr ustida quyidagi amalni istalgancha bajarish mumkin:
- Satrning boshidan k ta belgini o'chiring
- Satrning oxiriga istalgan k ta belgini qo'shing (belgining satr ichida bor-yo'qligi muhim emas)
Ushbu amaldan istalgan miqdorda - foydalanishga ruxsat berilsa, minimum necha qadamda satrni dastlabki holatga qaytarish mumkin?
Yagona qatorda lotin alifbosining kichik harflaridan iborat S satri kiritiladi. Satr uzunligi 1 000 000 dan oshmaydi
0 ga teng bo'lmagan minimum amallar sonini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
abcabacd 3 |
3 |
| 2 |
abacaba 3 |
2 |
D. Qalamlar soni
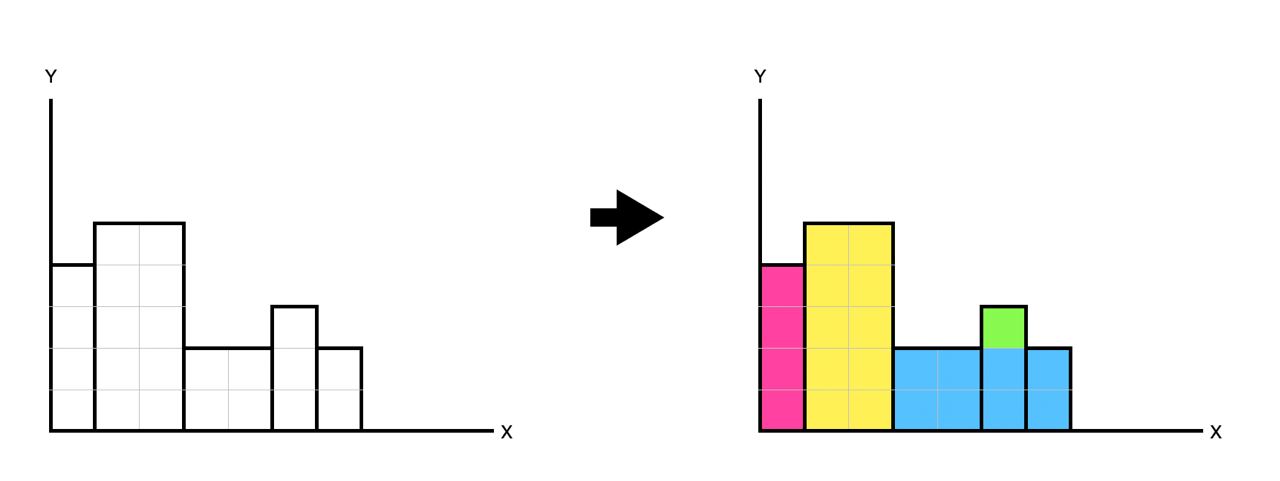
Xotira: 32 MB, Vaqt: 1000 msRoboboyda ikki o'lchovli koordinatalar sistemasida \(N\) ta to'rtburchak bor. Har bir to'rtburchakning eni (\(W_i\)) va bo'yi (\(H_i\)) berilgan. Har bir to'rtburchakning pastki qismi \(X\) o'qida joylashgan bo'lib, dastlabki to'rtburchakning chap tomoni \(Y\) o'qiga tegib turgan holda, qolgan to'rtburchaklarning chap tomoni esa o'zidan oldingi to'rtburchakka tegib turgan holda joylashgan.
Roboboy barcha to'rtburchaklarning ichini bo'yamoqchi, qaysi rangda bo'yashi muhim emas. Ammo Roboboyning bo'yash uchun mo'ljallangan qalamlari bir martalik bo'lib, faqat to'rtburchak shakldagi 1 ta maydonni bo'yay oladi.
Barcha to'rtburchaklarni ichini bo'yash uchun Roboboyga eng kamida nechta qalam kerak bo'lishini aniqlang!
Kirish faylining dastlabki satrida bitta butun son, \(N(1 \le N \le 250 \ 000)\) soni kiritiladi. Keyingi N ta qatorda 2 tadan butun son \(W_i, H_i (1 \le W_i, H_i \le 10^9)\) to'rtburchaklarning o'lchamlari kiritiladi.
Barcha to'rtburchaklarni ichini bo'yash uchun Roboboyga kerak bo'ladigan eng kam qalamlar sonini chop eting!
1-test, ajralib turishi uchun har xil rangli qalamlardan foydalanildi:
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 1 4 2 5 2 2 1 3 1 2 |
4 |
E. K belgili satr
Xotira: 32 MB, Vaqt: 1000 msSizga K soni hamda S satri berilgan. Agar satr uzunligi K dan katta bo'lsa, satrning boshidan K ta belgini va undan keyin … (uch nuqta) qo'ygan holatda chop eting, aks holda satrni o'zini chop eting.
1-qatorda \(K ( 1\le K \le 100)\) soni kiritiladi.
Keyingi qatorda ingliz alifbosining kichik harflaridan tashkil topgan S satri kiritiladi. S satri uzunligi 100 dan oshmaydi.
S satr bo'sh emasligi kafolatlanadi.
Javobni chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 hello |
hello |
| 2 |
11 robocontestuz |
robocontest... |
| 3 |
7 aaa |
aaa |
F. Daraxtdagi LIS
Xotira: 64 MB, Vaqt: 1000 msN ta tugundan tashkil topgan daraxt mavjud. \(i-\)yo'l \(u_i\) va \(v_i\) tugunlarni o'zaro bog'laydi va qiymati \(a_i\) ga teng. 1 dan N gacha bo'lgan har bir k butun soni uchun quyidagini aniqlang:
- Yo'llarga yozilgan butun sonlarni 1-yo'ldan k-yo'lgacha bo'lgan eng qisqa yo'l bo'ylab ular paydo bo'ladigan tartibda qatorlab ketma-ketlik hosil qilamiz. Ushbu ketma-ketlikning eng uzun ortib boruvchi pastki ketma-ketligi (LIS)ining uzunligini toping.
Bu yerda uzunligi \(L\) boʻlgan \(A\) ketma-ketlikning eng uzun ortib boruvchi pastki ketma-ketligi \(M\) ning mumkin boʻlgan eng katta qiymatiga ega boʻlgan \(A_{i_1}\) ,\(A_{i_2}\) ,...,\(A_{i_M}\) qatori boʻlib, \(1≤i_1 <i_2 <...<i_M ≤L\) va \(A_{i_1} < A_{i_2} <...< A_{i_M}\) bo'ladi.
Birinchi qatorda N butun soni kiritiladi.
Keyingi qatorda N ta butun son a massiv elementlari kiritiladi
Keyingi N-1 ta qatorning har birida 2 tadan butun son \(u_i\) va \(v_i\) kiritiladi.
- \(2 \le N \le 2*10^5\)
- \(1 \le a_i \le 10^9\)
- \(1 \le u_i, v_i \le N\)
- \(u_i \neq v_i\)
- Graf daraxt ekanligi kafolatlanadi.
- Barcha qiymatlar butun sonlardir.
N qatorni chop eting. k-chi qator, 1-yo'ldan k-yo'lgacha bo'lgan eng qisqa yo'ldan olingan ketma-ketlikning eng uzun o'sib boruvchi pastki ketma-ketligi uzunligini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
10 1 2 5 3 4 6 7 3 2 4 1 2 2 3 3 4 4 5 3 6 6 7 1 8 8 9 9 10 |
1 2 3 3 4 4 5 2 2 3 |
G. O'quv mashg'uloti
Xotira: 32 MB, Vaqt: 1000 msBugun N ta askarlar o'quv-mashg'ulot maydoniga amaliyot uchun kelishdi. Maydonning omborxonasida 1 dan M gacha raqamlangan M turdagi avtomat mavjud. Har bir askar A[i] turdagi avtomatda mashg'ulot o'tkazishni xohlaydi. Maydonda K ta otish maydonchasi mavjud. Kichik maydonchalarning har birida 1 kishi faqatgina bitta avtomatdan foydalangan holda mashg'ulot o'tkaza oladi. Boshida hamma kichik maydonchalar bo'sh.
i-askarning navbati kelgan vaqt agar kichik maydonchalarning birortasida u yoqtirgan turdagi avtomat bo'lsa, shu maydonchada mashg'ulot o'tkazadi. Mavjud bo'lmasa, omborxonadan o'zi yoqtirgan turdagi avtomatni olib chiqadi hamda istalgan bo'sh maydonga joylashtiradi. Agar hamma maydoncha band bo'lsa, istalgan birorta maydonchada turgan qurolni omborxonaga qo'yib o'zi istagan turdagi qurolni joylashtirishi mumkin. Eski qurolni omborxonaga qo'yish va yangisini olib kelish uchun bir marta borib kelish kifoya (borishda eskisini tashlab, qaytayotganda yangisini olib keladi). Mashg'ulotni tugatgandan so'ng, qurol shu maydonchada qoladi.
Har bir askar navbatma-navbat mashg'ulot o'tkazsa va optimal harakat qilishsa, eng kamida necha marotaba omborxonaga borish kerak bo'ladi?
Birinchi qatorda 3 ta butun son M, K, N - qurollar soni, kichik maydonchalar soni va askarlar soni kiritiladi.
Keyingi qatorda M ta butun son kiritiladi, i-son i-askar qaysi avtomatni yoqtirishini ifodalaydi.
1 ≤ M ≤ 500 000
1 ≤ K ≤ N ≤ 100 000
Barcha askar optimal harakat qilsa, minimum necha marta omborxonaga borish kerak bo'lishini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 2 7 2 3 1 2 1 2 3 |
4 |
| 2 |
5 3 8 1 5 3 5 3 2 4 2 |
5 |
H. Asadbekning gullari
Xotira: 16 MB, Vaqt: 1000 msAsadbek gullarni parvarishlashni yoqtiradi. U “Ci plus plusium” gullaridan o‘zining qator joylashgan \(n\) ta tuvagining barchasiga ekdi. Birinchi kuni barcha gullarning bo‘yi 0 deb hisoblasa bo‘ladi. Shu kundan boshlab har kuni Asadbek:
- shunday \([l, r]\) oraliqni tanlaydiki, shu oraliqdagi barcha tuvaklardagi gullarning bo‘yi bir xil bo‘lsin;
- \([l+1,r-1]\) oraliqdagi barcha tuvaklarga suv quyadi. Keyingi kungacha shu oraliqdagi tuvaklarda joylashgan gullar 1 birlikka ga o‘sadi.
Misol, \(n=6\) uchun mos ravishda 1-2-3-kunlardagi gullarning bo‘yini quyidagicha tasvirlash mumkin:

1-kuni \([1,6]\) oraliq tanlangan va \([2,5]\) oraliqdagi tuvaklarga suv quyilgan.
2-kuni \([3,5]\) oraliq tanlangan va \([4,4]\) oraliqdagi tuvaklarga suv quyilgan.
0 yoki bir necha kundan so‘ng, Asadbek o‘zining gullari bilan maqtanmoqchi bo‘lib, har bir gulining bo‘yini \(A\) massiviga yozib, uni sizga berdi (\(A_i=i\)-tuvakdagi gulning bo‘yi). Ammo ba’zi gullarining bo‘ylarini eslay olmagani uchun, ularning bo‘ylarini o‘rniga -1 sonini yozdi.
Sizning vazifangiz Asadbek bergan ma’lumotlarga ko‘ra, bugungi kunda uning gullari necha xil ko‘rinishda bo‘lishi mumkinligini sanashdir. Agarda Asadbek sizni aldagan bo‘lsa, 0 chiqaring.
Natija katta bo‘lishi mumkinligi sababli, natijani \(10^9+7\) ga bo‘lingandagi qoldig‘ini chiqaring.
Kirish oqimining birinchi qatorida bitta butun son - \(n(1 \le n \le 10^4)\) kiritiladi.
Keyingi qatorda \(n\) ta butun son - Asadbek sizga bergan \(A\) massiv elementlari kiritiladi. Massiv elementlari yoki -1 yoki \(10^4\) dan oshmaydigan butun manfiy bo‘lmagan sonlardir.
Hozir Asadbekning gullari necha xil ko‘rinishda bo‘lishi mumkin ekanligini \(10^9+7\) ga bo‘lgandagi qoldig‘ini chiqaring. U aldagan bo‘lsa 0 chiqaring.
Birinchi testda:
Hech qanday usulda \(n=4\) uchun bo‘yi 3 bo‘lgan gul o‘stirib bo‘lmaydi. Demak Asadbek aldagan.
Ikkinchi testda:
Asadbekning gullari quyidagi 3 xil ko‘rinishda bo‘lishi mumkin:
\([0,1,2,2,1,0]\);
\([0,1,2,1,1,0]\);
\([0,1,2,1,0,0]\).
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 -1 -1 3 -1 |
0 |
| 2 |
6 -1 -1 2 -1 -1 -1 |
3 |
I. Kompyuter xonasida
Xotira: 32 MB, Vaqt: 1000 msTATU ning E blok 111-xonasi, kompyuter xonasidir. Va u yerda \(N\) ta kompyuter bir qator chiziqda joylashgan. Tez orada u xonada Shokirov Shodmon domlaning darsi boshlanadi. Shuning uchun ham hali xonaga kirmagan talabalar NB(darsda bo`lmadi) olmasligi uchun xonaga kirishni tezlashtirishlari lozim. Ammo aniqlandiki, bu xonadagi ba'zi kompyuterlardan foydalanib bo`lmaydi. Chunki u kompyuterlardan hozir kimdir foydalanyapti yoki ular buzuq. Xonaga kelgan har yangi talaba eshikka eng yaqin foydalanib bo`ladigan kompyuter oldiga o`tiradi va u kompyuterni yangi keladiganlar uchun foydalanilmaydigan qiladi. 1-kompyuter eshikka eng yaqin hisoblanadi.
Agar dars boshlanmasidan oldin xonaga \(K\) ta bola kirsa, ular band qiladigan kompyuter o`rinlarini o`sish tartibida ekranga chiqaring. Foydalanib bo`ladigan kompyuterlar yetarlicha ekanligi kafolatlanadi.
Birinchi qatorda ikkita butun son - \(N\) va \(K(1 \leq K \leq N \leq 2*10^5)\) sonlari kiritiladi.
Keyingi qatorda \(N\) ta butun son kiritiladi. \(i\)-son: \(1\) bo`lsa, bu kompyuterdan foydalanib bo`lmasligini, \(0\) bo`lsa esa bu kompyuterdan foydalanib bo`lishini anglatadi.
Darsga ulgurgan talabalar o`tiradigan kompyuter o`rinlarini orqali chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
7 3 1 0 1 1 0 0 1 |
2 5 6 |
| 2 |
3 2 0 0 0 |
1 2 |