A. Shaxmat
Xotira: 16 MB, Vaqt: 1000 msn × n o’lchamli shaxmat doskasida shaxmat figurasi bor. (x0, y0) katakdan (x1, y1) ga borish uchun eng kam yurishlar sonini toping. (imkoni bo’lmasa -1 chiqaring)
shaxmat figurasi quyidagilar bo’lishi mumkin: Ot, Shoh, Fil, To’ra va Farzin.
Birinchi qatorda n(1 ≤ n ≤ 1000) va figuraning nomi. ("Ot", "Shoh", "Farzin", "Fil", "Tora").
Ikkinchi qatorda x0 va y0 (1 ≤ x0, y0 ≤ n) kiritiladi.
Uchinchi qatorda x1 va y1 (1 ≤ x1, y1 ≤ n) kiritiladi.
Bitta qatorda eng kam yurishlar sonini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 Shoh 4 4 1 5 |
3 |
B. FibORacci
Xotira: 16 MB, Vaqt: 1000 msFibORacci ketma-ketligi deb quyidagi ketma-ketlikni aytamiz:
f(0) = a
f(1) = b
f(n) = f(n-1) OR f(n-2), n > 1. Bu yerda OR – Bitwise OR(razryadli yoki) amali.
Sizning vazifangiz f(m) ning qiymatini topish.
Bitta qatorda a, b va m nomanfiy butun sonlari kiritiladi. (0 ≤ a, b, m ≤ 1018)
Bitta qatorda f(m) ning qiymatini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 4 2 |
7 |
C. Olimpiada
Xotira: 16 MB, Vaqt: 1000 msO’zbekistonda m ta shahar bor (m = 2k) va m ta shaharda jami n ta o’quvchi bor. Har bir o’quvchining o’zini bilim darajasi bor. (i – o’quvchining bilim darajasi ai , ya’ni i – o’quvchi ai ta algoritm biladi). Ikkita o’quvchi o’zaro bellashishsa bilim darajasi yuqoriroq o’quvchi g’olib bo’ladi. (Barcha o’quvchilarning bilim darajalari har xil ekanligi kafolatlanadi).
O’quvchilar 2 ta olimpiadada qatnashishdi. (Beruniy va Al-Xorazmiy olimpiadasi)
Beruniy olimpiadasi tartibi quyidagicha (Futbol bo’yicha Jahon Chempionati tartibiga o’xshash):
Har bir shaharda alohida olimpiada o’tqaziladi. G’olib o’quvchi keyingi turga o’tadi (o’z shahridagi bilim darajasi eng yuqori bo’lgan o’quvchi). Keyingi turda 1-shaharlik o’quvchi 2-shaharlik o’quvchi bilan, 3-shaharlik o’quvchi 4-shaharlik o’quvchi bilan va hokazo bellashishadi. G’oliblar keyingi turga o’tib 1-juftlik g’olibi 2-juftlik g’olibi bilan va hokazo bellashishadi. Yakunda finalda yutgan o’quvchi 1-o’rin, yutqazgan 2-o’rin. Yarim finalda yutqazgan o’quvchilar 3-o’rin uchun bellashishadi. Yaxshiroq tushunish uchun izohga qarang.
Al-Xorazmiy olimpiadasi tartibi quyidagicha:
Barcha n ta o’quvchilar bir joyga to’planishadi va bilim darajasi eng yuqori bo’lgan o’quvchilarga mos ravishda 1, 2 va 3-o’rinlar beriladi.
Sizning vazifangiz ikkala olimpiadaning g’oliblarini aniqlash.
Birinchi qatorda m va n kiritiladi. (4 ≤ m ≤ 215, m ≤ n ≤ 2×105)
Ikkinchi qatorda n ta natural sondan iborat a massiv - o’quvchilarning bilim darajalari kiritiladi (1 ≤ a[i] ≤ 109)
Uchinchi qatorda ham n ta natural sondan iborat c massiv kiritiladi. (c[i] – i-o’quvchining qaysi shahardanligi, 1 ≤ c[i] ≤ m)
Har bir shaharda kamida bitta o’quvchi yashashi kafolatlanadi.
Birinchi qatorda 3ta natural son. 1-olimpiadaning g’oliblarini raqamlarini chiqaring. Avval 1 - o’rin egasining raqami, keyin 2, keyin 3-o’rinning raqamini chiqaring.
Ikkinchi qatorda ham xuddi shu tartibda 2-olimpiadaning g’oliblarini chiqaring.
1 – shaharlik o’quvchilar – {7, 9}
2 – shaharlik o’quvchilar – {10}
3 – shaharlik o’quvchilar – {3, 14}
4 – shaharlik o’quvchilar – {4, 5, 11}
5 – shaharlik o’quvchilar – {6, 13}
6 – shaharlik o’quvchilar – {1}
7 – shaharlik o’quvchilar – {2, 12}
8 – shaharlik o’quvchilar – {8}
Avval Beruniy olimpiadasi g’oliblarini topamiz.
1 – shaharning olimpiadasi g’olibi 9-o’quvchi. Sababi uning bilim darajasi 42, 7-o’quvchining bilim darajasi esa 5. 9-o’quvchi keying turga o’tadi.
2 – shaharning olimpiadasi g’olibi 10-o’quvchi chunki shaharda undan boshqa o’quvchi yo’q.
Shunday qilib o’z shahrining g’olib o’quvchilari – {9, 10, 3, 11, 6, 1, 12, 8}. Keyingi turda 9-o’quvchi 10-o’quvchi bilan, 3-o’quvchi 11-o’quvchi bilan va h.k. bellashishadi. Yarim finalga kelgan o’quvchilar {10, 3, 6, 12}. Birinchi yarim finalda 10 va 3-o’quvchilar bellashishadi. Ikkinchi yarim finalda 6 va 12. Finalga chiqishdi – {10, 12}. 3-o’rin uchun bahsda bellashadi {3, 6}. Shunday qilib 1-o’rin – 10, 2-o’rin – 12 va 3-o’rin – 3-raqamli o’quvchilar.
Endi Al-Xorazmiy olimpiadasi g’oliblari:
1-o’rin – 10-raqamli o’quvchi
2-o’rin – 12-raqamli o’quvchi
3-o’rin – 9-raqamli o’quvchi
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
8 14 16 8 29 12 15 20 5 32 42 85 22 53 11 21 6 7 3 4 4 5 1 8 1 2 4 7 5 3 |
10 12 3 10 12 9 |
D. Maksimum uzunlik
Xotira: 16 MB, Vaqt: 1000 msQuyidagidek belgilash kiritaylik.
edge (rus tilida “Ребро”) – a va b orasida edge bor degani – a va b shaharlar orasida to’g’ridan – to’g’ri ikki tomonli yo’l bor degani. Ya’ni a va b qo’shni shaharlar. Har bir edgening uzunligi 1 km.
path (rus tilida “Путь”) – a dan b ga boradigan path degani – a shahardan b shaharga boruvchi eng qisqa yo’l (bir yoki bir nechta edgedan o’tuvchi eng qisqa yo’l). Pathning uzunligi deb, ushbu path nechta edgedan o’tganiga aytiladi. Yoki a va b orasidagi masofa.
Masalan rasmda 1 va 4 orasida edge bor hamda 2 va 5 orasida edge bor. Yoki 3 va 5 orasidagi pathning uzunligi 3ga teng.
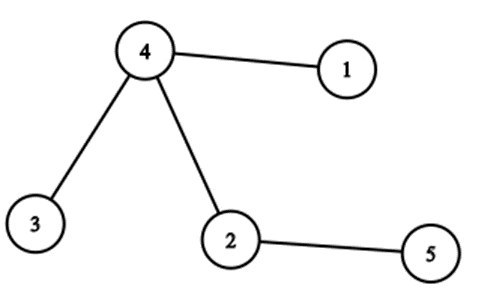
Baytlandiyada n ta shahar bor. Ular orasida n-1 ta edge bor. Ixtiyoriy shahardan boshqa bir shaharga faqat bitta path bor. Sizga q ta so’rov va har bir so’rovda x natural soni beriladi. Sizning vazifangiz x-shahardan eng uzoqda joylashgan shahardan x ga eng yaqin bo’lgan shaharlar orasidagi pathning uzunligi maximum nechi bo’lishi mumkin? Masalan, x dan eng uzoqda joylashgan shaharlardan biri a bo’lsin, x ga eng yaqin joylashgan shaharlardan biri b bo’lsin. U holda a dan b ga boruvchi pathning uzunligi eng ko’pi bilan nechi bo’lishi mumkin?
Masala shartiga tushunmaganlar uchun avval graflar teoriyasi hamda daraxtlar haqida o’qib chiqish tavsiya etiladi:
Graflar teoriyasi
Daraxtlar
Bitta qatorda n va q butun sonlar. (2 ≤ n ≤ 2×105, 1 ≤ q ≤ 2×105). Shaharlar 1 dan n gacha raqamlangan.
Keyingi n-1 ta qatorda ikkitadan butun a va b sonlari – a va b shaharlar orasida edge, ikki tomonli to’g’ridan – to’g’ri yo’l bor degani. (1 ≤ a, b ≤ n).
Keyingi q ta qatorda bittadan x butun son. (1 ≤ x ≤ n)
Har bitta so’rov uchun alohida qatorda bittadan butun son – x ga eng yaqin shahardan x dan eng uzoqdagi shahargacha masofalarning maximali.
2 dan eng uzoqdagi shahar 1, eng yaqini 5 bo’lganda javob maximal bo’ladi. 1 dan 5 gacha masofa 3 ga teng.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 2 1 4 4 2 4 3 2 5 2 1 |
3 2 |
E. Massiv
Xotira: 16 MB, Vaqt: 1000 msn ta elementdan iborat a massiv hamda k natural son berilgan. a ning nechta qism to’plamidagi sonlar yig’indisi k ga bo’linadi?
Aniqrog’i nechta 1 ≤ i ≤ j ≤ n indexlar borki ai + ai+1 + … + aj son k ga bo’linadi?
Birinchi qatorda n va k natural sonlar. (1 ≤ n ≤ 105, 1 ≤ k ≤ 109)
Keyingi qatorda n ta butun son a massivning elementlari kiritiladi. (1 ≤ a[i] ≤ 109)
Masalaning javobi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 3 1 2 5 3 |
2 |
F. Yo'l
Xotira: 16 MB, Vaqt: 1000 msn × n o’lchamli jadvalda (x0, y0) katakdan (x1, y1) ga nechi xil usulda borish mumkin? Masalan ushbu rasmda (1, 2) dan (3, 3) ga boruvchi yo’l tasvirlangan.
LDRDLDRRRUUULDD
LDRRURDDDLLLURR (Rasmdagi yo’l)
LDDDRRRUUULDLDR
LDDDRUURURDDDLU
Yo’l har bir katakdan aynan bir marta o’tishi shart.
Birinchi qatorda n natural son. (2 ≤ n ≤ 5).
Ikkinchi qatorda x0 va y0 (1 ≤ x0, y0 ≤ n).
Uchinchi qatorda x1 va y1 (1 ≤ x1, y1 ≤ n).
Bitta qatorda (x0, y0) dan (x1, y1) ga necha xil usulda borish mumkinligini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 1 2 3 3 |
4 |
G. Contest
Xotira: 32 MB, Vaqt: 2000 msIsfandiyor o’tgan bir oy ichida n ta kontestda qatnashishga ariza berdi. U har bir kontestning boshida masalalarni ko’rib chiqadi. Biroq Isfandiyor geometriya masalalarini judayam yomon ko’rganligi bois, agar kontestda bironta masala geometriya bo’lsa u bironta ham masala ishlamasdan kontestdan chiqib ketadi. Agar kontestda bironta geometriya masalalari yo’q bo’lsa u barcha masalalarni ishlaydi. Endi unda savol tug’ildi, u shu kungacha kamida va ko’pida nechta misol ishlagan?
Birinchi qatorda n va g, nechta contest o’tqazilgani hamda shu kungacha jami nechta geometriya masalalari qo’yilganligi. (1 ≤ n ≤ 1000, 1 ≤ g ≤ 3000)
Keyingi qatorda n ta butun son, har bir kontestda nechta masala qo’yilganligi. (1 ≤ a[i] ≤ 5000)
Barcha masalalar yig'indisi g dan kichik emas, a1 + a2 + ... + an >= g
Bitta qatorda ikkita butun son, Isfandiyor kamida va ko’pida nechta masala yechganini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 3 4 3 5 1 7 |
4 17 |
H. Isfandiyor algebra darsida
Xotira: 16 MB, Vaqt: 1000 msIsfandiyorga algebra fanidan quyidagi vazifa uy vazifasiga berildi:
\(f(x) = x^5 + 8x^4 - 5x^3 + 3x^2 + x - 12\), bo’lsa \(f(n)\) ni toping.
Ammo u dangasaligi uchun bu ishni o’zi qilgisi kelmayapti. Siz unga yordam bering.
Bitta \(n\) butun son. \(\lvert n \rvert \le 10\)
Bitta qatorda \(f(n)\) ning qiymatini chiqaring.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 |
-4 |