A. Teskari kodlash 2

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Zarif odatdagi kodlash turlaridan charchagan holda teskari kodlashga bo'lgan qiziqishi osha boshladi.

Unga quyidagicha savol tug’ildi, namunadan foydalangan holda shablonni tezda anglab olishga sizning qurbingiz yetarmikin?

Na’muna:

N	M
10	55
20	210
5	15
0	0
1	1
2	3

Sizning vazifangiz namunadan foydalangan holda shablonni aniqlash va berilgan so’rovdagi N va M juftliklar shablonga mosligini tekshirishdan iborat.

Kiruvchi ma'lumotlar:

INPUT.TXT kirish faylining dastlabki qatorida bitta butun son, \(T (1 ≤ T ≤ 50)\) soni kiritiladi. Keyingi T ta qatorning har birida bo’sh joy bilan ajratilgan holda ikkitadan butun son, \(N (0 ≤ N ≤ 1000)\) va \(M (0 ≤ M ≤ 10^6)\) sonlari kiritiladi.

Chiquvchi ma'lumotlar:

OUTPUT.TXT chiqish faylining yagona satrida berilgan T ta juftlikdagi N va M sonlari uchun, sonlar yuqoridagi shablonga mos bo’lsa 1 aks holda 0 sonini chiqaring!

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	4 10 55 4 11 2 3 6 21	1011

B. Bo'sh massiv

Xotira: 64 MB, Vaqt: 1000 ms

Masala

Sizga faqat 0 va 1 lardan tashkil topgan massiv beriladi. Siz quyidagi amalni istalgancha bajara olasiz.

Massivning istalgan kamaymaydigan tartibdagi prefixni tanlab uni o'chirish.

Sizning vazifangiz shu massivni iloji boricha kam amal bajarish orqali bo'sh holatga keltirish

Kiruvchi ma'lumotlar:

Birinchi qatorda testlar sonini ifodalovchi \(T\) soni kiritiladi. \((1 ≤ T ≤ 20000)\)
Har bir testning birinchi qatorida \(N\) - massivdagi elementlar soni. \((1 ≤ N ≤ 200000)\)
Har bir testning ikkinchi qatorida faqat 0 yoki 1 dan iborat \(N\) ta son kiritiladi.
\(N\) ning barcha testlardagi yig'indisi 200000 dan oshmaydi.

Chiquvchi ma'lumotlar:

Har bir test uchun massivni o'chirish uchun ketadigan minimal amallar sonini chiqaring

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 4 0 0 1 1 2 1 0 2 0 0	1 2 1

C. Qat'iyatli son

Xotira: 16 MB, Vaqt: 1000 ms

Masala

length(A) funksiyasi A sonining 10 lik sanoq tizimida ifodalanishidagi raqamlar soniga teng bo'lsin.
Qat'iyatli son deb quyidagi sonlarga aytiladi:
length(A) = 1 bo'lgan barcha nomanfiy sonlar qat'iyatli sondir.
length(A) > 1 bo'lgan barcha nomanfiy sonlar qat'iyatli bo'lishi uchun quyidagi ikki shartni bajarishi kerak

A soni length(A) ga qoldiqsiz bo'linishi kerak
A / length(A) soni ham qat'iyatli son bo'lishi kerak

Sizning vazifangiz [L, R] oralig'iga tegishli nechta qat'iyatli son borligini topishdan iborat.

Kiruvchi ma'lumotlar:

INPUT.TXT kirish faylining dastlabki qatorida bitta butun son, \(T (1 ≤ T ≤ 200)\) testlar soni kiritiladi.
Keyin har bir test uchun alohida qatorda ikkitadan butun son, \(L\) va \(R (0 ≤ L, R <= 10^{18})\)

Chiquvchi ma'lumotlar:

OUTPUT.TXT chiqish faylida har bir test uchun alohida qatorda masala javobini chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	5 7 25 33 48 1 100 99 103 0 1000000	10 3 26 0 96

D. Ketma-ketlik 235

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Tub bo’luvchilari faqatgina 2,3,5 lardan iborat bo’ladigan N - natural sonni toping.

Kiruvchi ma'lumotlar:

INPUT.TXT kirish faylining dastlabki satrida bitta butun son, \(T (1 ≤ T ≤ 1000)\) testlar soni kiritiladi.
Keyingi \(T\) ta qatorda bittadan butun son, har bir test uchun \(N (1 ≤ N ≤ 12500)\) soni kiritiladi.

Chiquvchi ma'lumotlar:

OUTPUT.TXT chiqish faylida har bir test uchun alohida qatorda bittadan butun son, masalaning javobini chop eting.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	10 1 2 3 4 5 6 7 8 9 10	1 2 3 4 5 6 8 9 10 12

E. Kvadrat

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Dekart koordinatalar sistemasida to’rtburchak berilgan. To’rtburchakning kvadrat yoki kvadrat emasligini aniqlang.

Kiruvchi ma'lumotlar:

Birinchi qatorda T butun son. Testlar soni (1 ≤ T ≤ 2∙10⁵)
Har bir bitta testda 1-qatorda to’rtburchak nuqtalarining X koordinatalari, 2-qatorda Y koordinatalari. (-10⁶ ≤X, Y ≤ 10⁶). Nuqtalar soat millari tartibida kiritiladi.

Chiquvchi ma'lumotlar:

Agar shakl kvadrat bo’lsa YES, aks holda NO chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 2 2 6 6 2 6 6 2 0 0 4 4 0 2 2 0 1 3 5 5 2 4 4 2	YES NO NO

F. Shaxmat

Xotira: 16 MB, Vaqt: 1000 ms

Masala

n × n o’lchamli shaxmat doskasida shaxmat figurasi bor. (x₀, y₀) katakdan (x₁, y₁) ga borish uchun eng kam yurishlar sonini toping. (imkoni bo’lmasa -1 chiqaring)
shaxmat figurasi quyidagilar bo’lishi mumkin: Ot, Shoh, Fil, To’ra va Farzin.

Kiruvchi ma'lumotlar:

Birinchi qatorda n(1 ≤ n ≤ 1000) va figuraning nomi. ("Ot", "Shoh", "Farzin", "Fil", "Tora").
Ikkinchi qatorda x₀ va y₀(1 ≤ x₀, y₀ ≤ n) kiritiladi.
Uchinchi qatorda x₁ va y₁ (1 ≤ x₁, y₁ ≤ n)kiritiladi.

Chiquvchi ma'lumotlar:

Bitta qatorda eng kam yurishlar sonini chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	5 Shoh 4 4 1 5	3

G. Azimjonning sevimli sonlari

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Azimjon tub qiymatlarni judayam yaxshi ko’radi. Agar natural son quyidagi shartlarni qanoatlantirsa Azimjon bu sonni sevimli son deb hisoblaydi:

Sonning yozilishida barcha ketma-ket joylashgan 3 ta raqamlar yig’indisi tub bo’lishi shart:

Sonning yozilishida barcha ketma-ket joylashgan 4 ta raqamlar yig’indisi tub bo’lishi shart:

Sonning yozilishida barcha ketma-ket joylashgan 5 ta raqamlar yig’indisi tub bo’lishi shart:

Kiruvchi ma'lumotlar:

INPUT.TXT kirish faylida bitta butun son, N(1 ≤ N ≤ 10⁶) soni kiritiladi.

Chiquvchi ma'lumotlar:

OUTPUT.TXT chiqish faylida Azimjonning sevimli soni bo’lgan eng kichik N xonali natural sonni chop eting.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1	1
2	2	10
3	3	101

H. Chumoli 2

Xotira: 10 MB, Vaqt: 1000 ms

Masala

Chumolilar yozda qish uchun uyiga qishgi oziq ovqatlarni to’plashini bilamiz. Bu gal ham chumolilar galasi qish uchun oziq ovqat to’plashga yo’lga chiqishda. Ular doim o’zi uchun tekis ya’ni bir chiziqda harakatlanadigan yo’lni qidirishadi va ular yo’lda bir o’rmonni uchratishdi. Ular endi bu o’rmon orqali o’ta olishadimi yo’qmi aniqlamoqchi. O'rmonda barcha daraxtlar aylana shakilda va hech bir ikkitasi bir biriga tegmaydi, Chumolilar o’rmonga kirmasdan ixtiyoriy bir nuqtadan o’rmonga qaraydi va o’rmonning nargi tarafi ko’rinsa demak o’ta olamiz degan xulosaga kelishadi aks holda ular boshqa yo’l qidirishadi. Sizning vazifangiz chumolilar o’rmon ichidan nargi tarafga tekis bir chiziqda daraxtlarga tegmasdan o’ta olishadimi yo’qmi aniqlash.

Kiruvchi ma'lumotlar:

Kirish fayilining dastlabki satirida \(N (1\leq N\leq 100)\) jami o'rmondagi daraxtlar soni.

Kiyingi \(N\) ta satirda uchtadan son \(x,y, r(-1000\leq x, y\leq 1000, 1\leq r\leq 1000)\) daraxtning markazini koordinatasi va daraxtning radusi berilgan.

Chiquvchi ma'lumotlar:

Chiqish fayilida agar chumolilar galasi o'rmondan bir tekis chiziqda kesib o'tishning imkoni bo'lsa Yes aks holda No so'zini chop eting.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 0 10 2 5 11 2 12.04 7 2	Yes
2	3 0 0 1 2.05 0 1 1.02 -1.9 1	No

I. Ketma-ketlik oxirgi raqam

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Jahongir ketma-ketliklarga qiziqadi. Bir kuni u ustozi bergan ketma-ketlik qaysi qonuniyat asosida ketishini aniqlash va shu ketma-ketlikning n-hadini oxirgi raqamini topish kerak edi. Jahongir qonuniyatni topdi! Qonuniyat shundan iborat ediki ketma-ketlikning dastlabki 3ta hadi beriladi. keyingi har bir had o'zidan oldingi 3ta hadning yig'indisiga teng. Endi sizning vazifangiz shu qonuniyat asosida ketma-ketlikning n-hadini topib Jahongirga yordam berishdan iborat

Kiruvchi ma'lumotlar:

Birinchi qatorda probel bilan ajratilgan holda 3ta butun son a, b, c va keyingi qatorda q butun sonlari kiritiladi. Keyingi qatorda probel bilan ajratilgan holda q ta butun son probel bilan ajratilgan holda kiritiladi. \((1 \leq a, b, c \leq 10^{18}, 0 < q \leq 1000, 1 \leq n \leq 10^{18})\)

Chiquvchi ma'lumotlar:

Chiqish faylida bitta qatorda q ta so'rov uchun ketma-ketlikning n-hadning oxirgi raqami probellar bilan ajratilgan holda chiqarilsin.

Izoh:

a-had ketma-ketlikning 0-hadi hisoblanadi

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1 4 8 6 4 5 6 7 8 9	5 6 4 5 5 4

J. Shaxzodning yangi yil sovg'asi

Xotira: 128 MB, Vaqt: 1000 ms

Masala

Qorbobo Shaxzodga Yangi yilda yangi MacBook PRO 14 sovg'a qildi. Endi Shaxzod eski MacBookidagi hamma ma'lumotlarini yangisiga ko'chirishi kerak. Buning uchun u qo'shimcha SSD diskidan foydalanmoqchi. Lekin diskga uning hamma ma'lumotlari sig'mas ekan. Azimjonning hisob-kitobiga ko'ra Shaxzod ma'lumotlarini 2 martada o'tkaza olar ekan. Buning uchun u papkalarining o'lchamini iloji boricha bir-biriga yaqin qilib 2 ga ajratishi kerak. Bu ishni Azimjon osongina bajara oldi, siz ham urinib ko'ring ;)

Shaxzodning eski MacBookida hamma papkalari 0 dan boshlab raqamlab chiqilgan. 0 papka root hisoblanadi, ya'ni barcha fayl va boshqa papkalar 0 papkada joylashgan. 2 qismga ajratayotganda faqat 1 ta papkani 1 marta ko'chirish mumkin, ko'chirishda papkaning ichidagi barcha fayllar va papkalar birgalikda ko'chadi. Fayllarni ko'chirish yoki bir nechta papkani ko'chirish ma'lumotlar chalkashib ketishiga olib keladi.

Kiruvchi ma'lumotlar:

N natural soni va ikkinchi qatorda N ta butun sondan iborat A massiv beriladi. A massivning i-elementi i-papka qaysi papkaning ichida turganligini bildiradi, 0 papka uchun bu qiymat har doim -1 ga teng.

Keyingi N ta qatorning har birida \(K_j\) soni va \(K_j\) ta nomanfiy butun son, mos ravishda j-papkadagi fayllar soni va fayl o'lchamlari beriladi. Fayl o'lchamlari \(10^9\) dan oshmaydi.
\(0<N\leq10^4; \space 0\leq K_j \leq 100; \space 0\leq j <N.\)

Chiquvchi ma'lumotlar:

Ma'lumotlarni ajratganda hosil bo'ladigan eng kichik farqni toping.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 -1 0 0 0 1 13 2 3 10	0
2	3 -1 0 0 1 1 1 13 2 3 10	1

K. Raqamli funksiya #2

Xotira: 16 MB, Vaqt: 1000 ms

Masala

\(f(x_1,x_2, \dots, x_n) = a_1x_1 + a_2x_2 + \dots + a_nx_n\) funksiya berigan.
Bu funksiyaning aniqlanish sohasi raqamlar to'plamidan iborat \((0 \leq x_i \le 9, \ 1 \le i \le n)\).
Funksiyaning barcha argumentlari turli raqamlarni qabul qilsa \((x_i \ne x_j, \ i \ne j)\), bu funksiyaning qabul qilishi mumkin bo'lgan maksimal va minimal qiymatlarini toping.

Kiruvchi ma'lumotlar:

Birinchi satrda bitta butun son \(n( 1 \le n \le 10)\) argumentlar soni kiritladi.
Ikkinchi satrda \(n\) ta butun son \(\{a_n\}\) to'plam kiritiladi \((-10^5 \le a_i \le 10^5)\).

Chiquvchi ma'lumotlar:

Raqamli funksiyaning maksimal va minimal qiymatlarini chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 5 3 -2	69 -15

L. N-xona #2

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Shaxboz daftariga N dan M gacha bo'lgan sonlarni yozib chiqdi. K - xonada qaysi raqam turgani uni qiziqtirib qo'ydi. Unga buni topishda yordam bering.

Kiruvchi ma'lumotlar:

Kirish faylida N va M sonlari birinchi qatorda kiritiladi. Bunda \(1 \le N \le M \le 10^{15}\)

Ikkinchi qatorda esa \(K(1 \le K \le 10^{18})\) soni kiritiladi.

Chiquvchi ma'lumotlar:

Chiqish faylida K-xonada qaysi raqam turganini chop eting.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	193 493 1308	-1
2	8 22 24	0

M. O'zgartirishlar

Xotira: 64 MB, Vaqt: 1000 ms

Masala

Sizda Q, N butun soni, Nta elementdan iborat \(A\) massiv va \(K\) butun soni bor. Siz berilgan massiv ustida quyidagi amallarni bajarishingiz mumkin.

\(L,R,K\)ko'rinishida so'rov beriladi, siz \(A\) massivning \([L, R]\)oralig'idagi har bir elementini \(K\) soniga o'zgartirib chiqing.

Yakunda hosil bo'lgan massivning yig'indisi juft yoki toq ekanligini aniqlang. Agar yig'indi juft bo'lsa ″YES″ so'zini aks holda ″NO″ so'zini chop eting.

Kiruvchi ma'lumotlar:

Kirish faylining birinchi satrida \(N,Q\) sonlari kiritiladi \((1 \le N, Q \le 2*10^5)\)
Ikkinchi satrda N ta butun son massiv elementlari kiritiladi \((1 \le A_i \le 10^9)\)
Keyingi \(Q\) ta qatorda mos ravishda \(L,R,K\) sonlari kiritiladi\((1 \le L,R \le N; 1\le K \le 10^9)\)

Chiquvchi ma'lumotlar:

Har bir so'rov uchun masalaning javobini chop eting.Bunda har bir harf istalgan formatda bo'lishi mumkin.

Izoh:

So'rovlar mustaqil va kelajakdagi so'rovlarga ta'sir qilmaydi.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	5 5 2 2 1 3 2 2 3 3 2 3 4 1 5 5 1 4 9 2 4 3	NO NO NO YES NO
2	4 4 1 6 9 10 1 2 3 1 3 2 2 4 1 1 4 6	NO YES YES YES

N. Noodatiy dasturlash musobaqasi

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Noodatiy dasturlash musobaqasida \(N\) ta o'quvchi ishtirok etmoqda. Uning boshqa musobaqalardan farqi shundaki bu musobaqa bir nechta raunddan tashkil topgan bo'ladi. Bunda masalani birinchi bo'lib ishlagan o'quvchi \(N\) ballni undan keyingilar mos ravishda 1 balldan kam ball olib boradi va har bir o'quvchi berilgan masalalarni ishlay olishi kafolatlanadi. Oxirgi bo'lib ishlagan ishtirokchi mos ravishda 1 ballni qo'lga kiritadi. Hozir sizga o'sha \(N\) nafar o'quvchining oxirgi raund oldidan ballari beriladi. Ulardan nechtasida g'oliblikni qo'lga kiritish imkoniyati borligini aniqlang.

Hech bir ikki o'quvchi bir vaqtda masalani ishlay olmaydi.

Agarda bir nechta o'quvchilarda ballar teng bo'lsa ularning barchasi g'olib deb topiladi.

Kiruvchi ma'lumotlar:

Kirish faylining 1-qatorida \(N(3 \le N \le 300 000)\) soni kiritiladi.

Keyingi \(N\) qatorda o'quvchilarning oxirgi raungacha to'plagan ballari.

Bunda ularning qiymatlari nomanfiy butun sonlar hamda 2000000 dan oshmaydi.

Chiquvchi ma'lumotlar:

Chiqish faylida yagona butun son nechta o'quvchida g'olib bo'lish imkoniyati borligini chop eting.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 8 10 9	3
2	5 15 14 15 12 14	4

O. Oxirgi yig'indi

Xotira: 256 MB, Vaqt: 2000 ms

Masala

Bu masalada sizga \(N\) o'lchamli \(A\) massiv berilgan. Siz esa uni oxirgi elementi qolguncha quyidagi amalni bajarishingiz kerak bo'ladi. Misol uchun sizga 5 ta elementdan iborat quyidagi massiv berilsa\( [1,2,3,4,5]. [1+2,2+3,3+4,4+5]\) va keyin\( [3,5,7,9] \)massivi hosil qilinadi. So'ng yana\( [3+5,5+7,7+9] = [8,12,16]\). Bu amal toki massiv elementi bitta qolguncha davom etadi. \([8+12,12+16] = [20,28]\) va oxirida \([20+28]\) qoladi. Shunda natija \(48\)teng bo'ladi. Siz ham sizga berilgan massivni oxirgi elementi qolguncha shu amallarni ketma - ket bajarib borasiz. Eng oxirida qolgan elementni ekranga chiqarishingiz kerak bo'ladi.

Kiruvchi ma'lumotlar:

Birinchi qatorda \(N\) soni \(N(3≤N≤10^6).\)

Ikkinchi qatorda \(N \) ta sondan iborat \(A\) massiv \(A[i] (1≤ A[i]≤10^9).\)

Chiquvchi ma'lumotlar:

Yagona qatorda masala yechimini ekranga chiqaring.

Izoh:

Masala yechimi juda katta bo'lib ketishi mumkin shuning uchun uni \(10^9+7\) ga bo'lgandagi qoldiqni ekranga chiqarishingiz kerak bo'ladi.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	5 1 2 3 4 5	48

P. G'aroyib yig'indi

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Sizga ikkita natural son beriladi. Sizning vazifangiz shu sonlar orasidagi 3ga bo'linadigan ammo 7 bo'linmaydigan sonlar yigindisini topish. Bunda ikkala chegara ham kiradi.

Kiruvchi ma'lumotlar:

INPUT.TXT kirish faylining yagona qatorida ikkita manfiy bo'lmagan butun sonlar berilgan, sonlar 10⁹ dan oshmaydi.

Chiquvchi ma'lumotlar:

OUTPUT.TXT chiqish faylining yagona satrida yig'indisini chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	26 443	27696
2	41 743	78402
3	67 542	41412

Q. Asadbekning gullari

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Asadbek gullarni parvarishlashni yoqtiradi. U “Ci plus plusium” gullaridan o‘zining qator joylashgan \(n\) ta tuvagining barchasiga ekdi. Birinchi kuni barcha gullarning bo‘yi 0 deb hisoblasa bo‘ladi. Shu kundan boshlab har kuni Asadbek:

shunday \([l, r]\) oraliqni tanlaydiki, shu oraliqdagi barcha tuvaklardagi gullarning bo‘yi bir xil bo‘lsin;
\([l+1,r-1]\) oraliqdagi barcha tuvaklarga suv quyadi. Keyingi kungacha shu oraliqdagi tuvaklarda joylashgan gullar 1 birlikka ga o‘sadi.

Misol, \(n=6\) uchun mos ravishda 1-2-3-kunlardagi gullarning bo‘yini quyidagicha tasvirlash mumkin:

1-kuni \([1,6]\) oraliq tanlangan va \([2,5]\) oraliqdagi tuvaklarga suv quyilgan.

2-kuni \([3,5]\) oraliq tanlangan va \([4,4]\) oraliqdagi tuvaklarga suv quyilgan.

0 yoki bir necha kundan so‘ng, Asadbek o‘zining gullari bilan maqtanmoqchi bo‘lib, har bir gulining bo‘yini \(A\) massiviga yozib, uni sizga berdi (\(A_i=i\)-tuvakdagi gulning bo‘yi). Ammo ba’zi gullarining bo‘ylarini eslay olmagani uchun, ularning bo‘ylarini o‘rniga -1 sonini yozdi.

Sizning vazifangiz Asadbek bergan ma’lumotlarga ko‘ra, bugungi kunda uning gullari necha xil ko‘rinishda bo‘lishi mumkinligini sanashdir. Agarda Asadbek sizni aldagan bo‘lsa, 0 chiqaring.

Natija katta bo‘lishi mumkinligi sababli, natijani \(10^9+7\) ga bo‘lingandagi qoldig‘ini chiqaring.

Kiruvchi ma'lumotlar:

Kirish oqimining birinchi qatorida bitta butun son - \(n(1 \le n \le 10^4)\) kiritiladi.

Keyingi qatorda \(n\) ta butun son - Asadbek sizga bergan \(A\) massiv elementlari kiritiladi. Massiv elementlari yoki -1 yoki \(10^4\) dan oshmaydigan butun manfiy bo‘lmagan sonlardir.

Chiquvchi ma'lumotlar:

Hozir Asadbekning gullari necha xil ko‘rinishda bo‘lishi mumkin ekanligini \(10^9+7\) ga bo‘lgandagi qoldig‘ini chiqaring. U aldagan bo‘lsa 0 chiqaring.

Izoh:

Birinchi testda:

Hech qanday usulda \(n=4\) uchun bo‘yi 3 bo‘lgan gul o‘stirib bo‘lmaydi. Demak Asadbek aldagan.

Ikkinchi testda:

Asadbekning gullari quyidagi 3 xil ko‘rinishda bo‘lishi mumkin:

\([0,1,2,2,1,0]\);

\([0,1,2,1,1,0]\);

\([0,1,2,1,0,0]\).

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	4 -1 -1 3 -1	0
2	6 -1 -1 2 -1 -1 -1	3

R. Chess

Xotira: 16 MB, Vaqt: 1000 ms

Masala

Ushbu masalada sizga \(8\times8\) maydonda bo'lib o'tadigan standart shaxmat o'yinining qaysidur jarayoni beriladi. Bu jarayonda yurish navbati sizga kelib qolgan va usha jarayonda faqatgina bitta yurish bilan raqibni mot qilishingiz kerak bo'ladi.

Misol: Agar siz oq toshlarda o'ynayotgan bo'lsangiz C5 da joylashgan ot ni D7 ga olib o'tish orqali raqibni bir marotaba yurishda mot qilish mumkun(1-test).

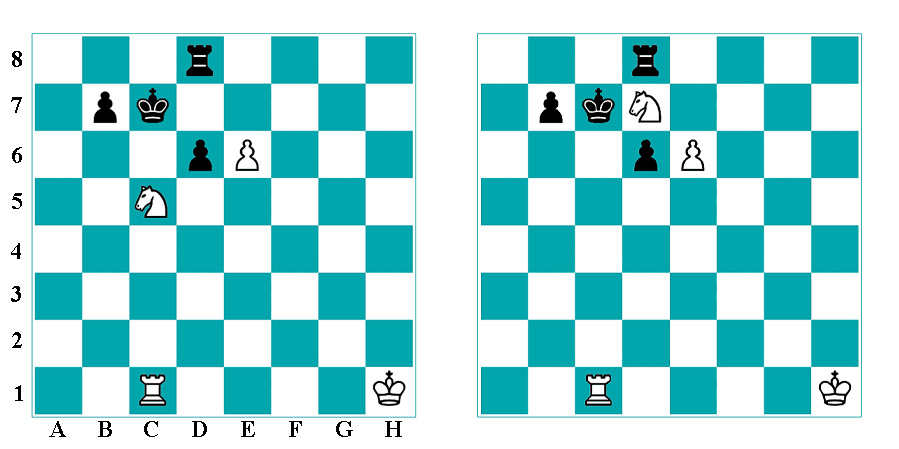
Shaxmat tosh donalari quyidagicha belgilanadi: King(shox) - K, Queen(farzin) - Q, Bishop(fil) - B, Knight(ot) - N, Rook(rux) - R va Pawn(piyoda) - P. Oq va qora toshlar mos ravishda katta kichik harflar bilan va bo'sh maydon nuqta bilan ifodalanadi.

Kiruvchi ma'lumotlar:

Kirish faylining dastlabki satrida \(k(0\leq k\leq 1)\) butun son ya'ni 0 yoki 1 bu mos ravishda siz o'yinni qora yoki oq toshlarda davom ettirishingizni anglatadi. Kiyin \(8\times8\) maydonda o'yin jarayoni tasvirlanadi.

Chiquvchi ma'lumotlar:

Siz shunday bir toshni boshqa maydonga kuchirish orqali shoxga hujum qilishingiz kerak natejada shox hujum ostida qolsin. Ko'chirilishi kerak bo'lgan toshning dastlabki va kiyingi koordinatasini mos ravishda probil bilan ajratilgan holda(agar bunday yechimlar bir nechta bo'lsa istalganini) chop eting. Yechim mavjudligi kafolatlanadi.

Izoh:

Piyoda harakati siz oq yoki qora toshlarda o'ynashingizdan qati nazar faqat bir tomonlama bo'ladi 2-testga qarang.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1 ...r.... .pk..... ...pP... ..N..... ........ ........ ........ ..R....K	C5 D7
2	0 ....K.R. .Pp..P.P ....Bb.. ..pP.... R.....p. .......p ....r... .......k	C7 C8