A. Robot

Xotira: 64 MB, Vaqt: 1000 ms
Masala

\(OX\) o'qida 0 - nuqtada robot turibdi. Uning keyingi \(n\) sekunddagi harakati \(a\) massiv orqali berilgan. Ya'ni:

  • \(a_i > 0\) bo'lsa, \(i\) - sekundda robot \(a_i\) qadam o'ngga yuradi
  • \(a_i < 0\) bo'lsa, \(i\) - sekundda robot \(a_i\) qadam chapga yuradi
  • \(a_i = 0\) bo'lsa, \(i\) - sekundda robot o'z joyida turadi.

\(n\) sekunddan keyin robot 0 - nuqtadan qancha uzoqlikda joylashishini toping.

Kiruvchi ma'lumotlar:

Birinchi qatorda \(a\) massiv uzunligini ifodalovchi \(n\) soni beriladi \((1 ≤ n ≤ 10^5)\). Keyingi qatorda esa \(n\) ta butun son - \(a\) massiv elementlari beriladi \((-10^9 ≤ a_i ≤ 10^9)\).

Chiquvchi ma'lumotlar:

Bitta butun son - masalaning javobini chiqaring.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
4
-2 3 5 -1
 
5
2 
3
2 3 -5
 
0

B. Golomb ketma-ketligi

Xotira: 64 MB, Vaqt: 1000 ms
Masala

Golomb ketma-ketligi \(G_1, G_2, \space \dots \space, G_n\) – \(i\) - elementi i soni ketma-ketlikda necha marta uchragani soniga teng bo’lgan o'suvchi ketma-ketlikdir. Ketma-ketlikning bir nechta dastlabki qiymatlari:
\([1, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 7, \space \dots]\).

Misol uchun, \(G_1 = 1\), sababi 1 soni ketma-ketlikda bir marta uchragan. Xuddi shu kabi \(G_4 = 3\), chunki 4 soni ketma-ketlikda 3 marta uchragan.

Golomb ketma-ketligini quyidagi formula orqali topish mumkin:

\(G_1 = 1\)
\(G_{i+1} = 1 +G_{i+1-G_{G_i}} \space\space i \ge1\)

Sizning vazifangiz Golomb ketma-ketligini dastlabki \(n\) ta hadi yig’indisini \((G_1 + G_2 + \dots + G_n)\) topishdan iborat.

Kiruvchi ma'lumotlar:

Bitta butun \(n\) soni \(( 1 \le n \le 10^9)\).

Chiquvchi ma'lumotlar:

Bitta butun son – masalaning javobi.

Izoh:

Ketma-ketlikning dastlabki 5 ta hadi: \({\{ 1, 2, 2, 3, 3}\}\). Ularning yig'indisi esa 11.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
5
 
11
2 
12
 
44

C. Daraxtlarni ulash

Xotira: 64 MB, Vaqt: 1000 ms
Masala

Daraxt deb bog’langan, \(n\) ta tugun va \(n-1\) ta shoxdan iborat grafga aytiladi.

Sizga mos ravishda \(n\) ta va \(m\) ta tugundan iborat bo’lgan ikkita daraxt berilgan. Birinchi daraxtning biror tugunini ikkinchi daraxtning biror tuguniga ulash orqali bitta yangi daraxt hosil qilindi. Sizning vazifangiz esa hosil bo’lgan daraxtda ixtiyoriy ikkita tugun orasidagi maksimal masofa eng kamida qancha bo’lishi mumkinligini topishdan iborat.

Ikki tugun orasidagi masofa deb, bu tugunlar orasidagi shoxlar soniga aytiladi.

Kiruvchi ma'lumotlar:

Birinchi qatorda bitta butun \(n\) soni - birinchi daraxt tugunlari soni \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda esa \(n-1\) ta \(u\) va \(v\) ko’rinishidagi juftliklar, ya’ni birinchi daraxt bog’lanishlari beriladi \((1 ≤ u, v ≤ n, u \ne v)\). Keyingi qatorda esa xuddi shu tartibda ikkinchi daraxt beriladi, dastlab \(m\) butun soni, so’ngra \(m - 1\) ta \(u\) va \(v\) juftliklar \((1 ≤ m ≤ 10^5, 1 ≤ u, v ≤ m, u \ne v)\).

Chiquvchi ma'lumotlar:

Bitta butun son – masalaning javobi.

Izoh:

Quyidagi rasmda birinchi daraxt sariq rangda, ikkinchi daraxt ko’k rangda berilgan, ularni bog’lovchi shox esa qizilda berilgan, yangi daraxtdagi eng uzun masofa 3.

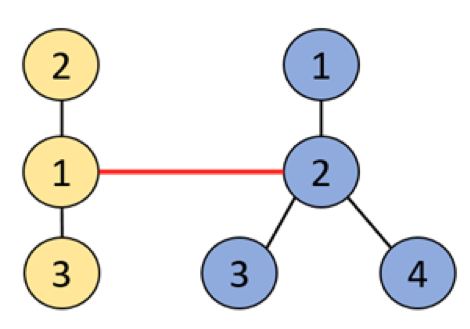
https://robocontest.uz/storage/images/m173.1.png

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
3
1 2
1 3
4 
1 2
2 3
2 4

3

D. Massiv

Xotira: 64 MB, Vaqt: 2000 ms
Masala

\(n\) ta elementdan iborat \(a\) massiv va \((x, y)\) ko'rinishidagi \(m\) ta juftliklar berilgan. Har bir \(i \space\space (1 ≤ i ≤ m)\) uchun massivni \(x_i\)- va \(y_i\)-elementlarini o'rnini almashtirish mumkin, bunda almashtirishlar soni cheklanmagan.

Sizning vazifangiz, yuqoridagi shartlarni qanoatlantirgan holda, \(a\) massivni leksikografik eng kichik holatga keltirishdan iborat.

Kiruvchi ma'lumotlar:

Birinchi qatorda ikkita butun son \(n\) va \(m\) beriladi \((1 ≤ n, m ≤ 10^5)\). Ikkinchi qatorda \(n\) ta butun son - \(a\) massiv elementlari beriladi \((1 ≤ a_i ≤ 10^9)\). Keyingi \(m\) ta qatorda esa \((x_i, y_i)\) juftliklar beriladi \((1 ≤ x_i < y_i ≤ n)\).

 

Chiquvchi ma'lumotlar:

Mumkin bo'lgan leksikografik eng kichik massivni chiqaring.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
5 2
7 3 5 1 4
1 3
3 4

1 3 5 7 4
2 
4 1
1 2 3 4
1 2

1 2 3 4

E. Dasturchi Shermat

Xotira: 64 MB, Vaqt: 2000 ms
Masala

Shermat robotni \(OX\) o'qi bo'yicha harakatlantiradigan dastur tuzdi va qanchadir vaqt o’tgach robot harakatlangan nuqtalarning koordinatalarini ekranga chiqardi. Lekin Shermat har doimgidek nimanidir esdan chiqargandi. Bu safar u probellarni esdan chiqaribdi. Endi robot jami \(k\) ta nuqtaga borgani va robot borgan ixtiyoriy ikkita qo'shni nuqtalar orasidagi masofa \([l,r]\) oraliqda bo’lishini (har bir \(i \space (1 ≤ i < k)\) uchun \(l ≤ |x_i - x_i+1| ≤ r\)) hisobga olib, sizdan hozirgi ma’lumotlarni necha xil usulda tiklash mumkinligini so'ramoqda.

Yodda tuting. Nuqtani koordinatasi nomanfiy butun son bo'lib, oldida nollar bo'lmasligi lozim (0 sonini o'zidan tashqari).

Kiruvchi ma'lumotlar:

Birinchi qatorda bitta butun \(t\) soni - testlar soni beriladi \((1 ≤ t ≤ 100)\). Keyingi \(t\) ta qatorda Shermat ekranga chiqargan nuqtalarni bildiruvchi \(x\) soni, shuningdek, \(l\), \(r\), va \(k\) sonlari beriladi. \((1 ≤ x ≤ 10^{18}, 0 ≤ l, r ≤ 10^{18}, 1 ≤ k ≤ 18)\).

 

Chiquvchi ma'lumotlar:

Har bir test uchun javobni alohida qatorda chiqaring.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
4
248 16 45 2
248 16 46 2
4444 1 5 2
10010 0 100000 2

1
2
0
2

F. Uchuvchi

Xotira: 64 MB, Vaqt: 2000 ms
Masala

Shaharda 1 dan \(n\) gacha raqamlangan \(n\) ta bino bor, \(i\)-bino balandligi \(h_i\). Uchuvchini \(m\) ta samolyoti bor, \(i\)- samolyot \(a_i\) balandlikkacha ko’tarila oladi.

Uchuvchi parvozini qaysidir \(s\) shaharda boshlab, \(t\) shaharda tugatadi, bunda \(s ≤ t\) bo’lishi lozim. Ya’ni u faqat o’ng tomonga ucha oladi. Uchuvchi samolyot ko’tarila oladigan balandlikdan baland binoga bora olmaydi.

https://robocontest.uz/storage/images/m176.1.png

Sizning vazifangiz har bir samolyot uchun, necha xil parvoz uyushtirish mumkinligini topishdan iborat

Kiruvchi ma'lumotlar:

Birinchi qatorda mos ravishda binolar soni va samolyotlar sonini bildiruvchi \(n\) va \(m\) sonlari beriladi \((1 ≤ n, m ≤ 10^5)\). Ikkinchi qatorda \(n\) ta butun son \(h_1, h_2, \space\dots\space, h_n\) beriladi. Uchinchi qatorda esa \(m\) ta butun son, \(a_1, a_2, \space\dots\space, a_m\) beriladi \((1 ≤ h_i, a_i ≤ 10^6)\).

Chiquvchi ma'lumotlar:

Har bir samolyot uchun turli xil parvozlar sonini toping.

Izoh:

Birinchi samolyot bilan uchuvchi quyidagicha parvozlarni amalga oshirishi mumkin: (1, 1), (3, 3), (5, 5), (5, 6), (6, 6).

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
6 3
1 3 2 4 1 2
2 3 4

5
9
21

G. Super chiptalar

Xotira: 128 MB, Vaqt: 2500 ms
Masala

Shermatning tug’ilgan kunida unga avtobus uchun chiptalar sovg’a qilishdi. Shermat boshida ozroq xafa bo’lgandi, lekin chiptalar oddiy emas balki super chiptalar ekanligini ko’rganidan keyin ancha taskin topdi.

Hozirda uning qo’lida \(m\) ta chipta bor va chiptalar 3 xil turga bo’linadi:
1. Bu chipta orqali \(a\) bekatdan \(b\) bekatgacha borsa bo’ladi.
2. Bu chipta orqali \(a\) bekatdan \([l,r]\) oraliqdagi ixtiyoriy bekatga borsa bo’ladi.
3. Bu chipta orqali esa \([l,r]\) oraliqdagi ixtiyoriy bekatdan \(a\) bekatga borsa bo’ladi.

Har bir chipta uchun avtobus qancha vaqt harakatlanishi ko’rsatilgan. Bekatlar soni jami \(n\) ta bo’lib, dastlab Shermat \(s\) - bekatda turibdi. Shermat \(s\) - bekatdan qolgan bekatlarga eng kamida qancha vaqt sarflab yetib olish mumkinligiga qiziqmoqda. Shaharda avtobus reyslari shunchalik ko’pki bekatdan bir avtobusdan tushib boshqasiga o’tirishga ketgan vaqtni 0 deb hisoblash mumkin.

Kiruvchi ma'lumotlar:

Birinchi qatorda 3 ta butun son - \(n\), \(m\), va \(s\) – bekatlar soni, chiptalar soni va Shermat turgan bekat beriladi \((1 ≤ n, m ≤ 10^5, 1 ≤ s ≤ n)\). Keyingi \(m\) ta qatorda chiptalar tavsifi kiritiladi va ular quyidagicha ifodalanadi:

  • \(1 \space a \space b \space t\) - bu birinchi turli chipta bo'lib, bu chipta orqali \(a\) bekatdan \(b\) bekatga \(t\) vaqtda borish mumkin.
  • \(2 \space a \space l \space r \space t\) - bu ikkinchi turli chipta bo'lib, bu chipta orqali \(a\) bekatdan \([l, r]\) oraliqdagi ixtiyoriy bekatga \(t\) vaqtda borish mumkin.
  • \(3 \space a \space l \space r \space t\) - bu uchinchi turli chipta bo'lib, bu chipta orqali \([l, r]\) oraliqdagi ixtiyoriy bekatdan \(a\) bekatga \(t\) vaqtda borish mumkin.
Chiquvchi ma'lumotlar:

Yagona qatorda probel bilan ajratilgan \(n\) ta sonni chiqaring, \(i\) - son \(s\) bekatdan \(i\) - bekatgacha borish mumkin bo'lgan eng qisqa vaqtga teng bo'lsin, agar borishni iloji yo'q bo'lsa \(-1\) chiqaring.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
3 5 1
2 3 2 3 17
2 3 2 2 16
2 2 2 3 3
3 3 1 1 12
1 3 3 17

0 28 12
Kitob yaratilingan sana: 25-Nov-24 13:46