A. Matritsaning maksimal yig'indisi
Xotira: 32 MB, Vaqt: 1000 msSizga 2N×2N o’lchamli matritsa berilgan. Siz 0 yoki bir necha marotaba matritsaning ixtiyoriy qatori yoki ixtiyoriy ustunini tanlab teskarisiga o’girishingiz mumkin. Shundan so’ng siz matritsaning yuqori chap burchagidagi N×N qism matritsaning yig’indisini hisoblaganingizda maksimal necha qiymatga ega bo’lishingiz mumkinligini aniqlang.
Masalan:
|
1 |
2 |
→ |
1 |
2 |
→ |
4 |
2 |
|
3 |
4 |
4 |
3 |
1 |
3 |
Dastlabki satrda bitta butun son, N(1 ≤ N ≤ 500), keyingi 2N qatorning har birida bo’sh joy bilan ajratilgan holda 2N ta [0, 106] oralig’idagi sonlar kiritiladi.
Ixtiyoriy marotaba matritsaning ixtiyoriy qatori yoki ixtiyoriy ustunini teskarisiga aylantirishdan so’ng yuqori chap N×N qism matrisada maksimal yig’indi necha bo’lishini aniqlang.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 1 2 3 4 |
4 |
| 2 |
2 112 42 83 119 56 125 56 49 15 78 101 43 62 98 114 108 |
414 |
B. Reyting
Xotira: 32 MB, Vaqt: 1000 msBaytlandiya mamlakatining BaytContest onlayn hakam tizimida har bir masala ishlangani uchun foydalanuvchiga manfiy bo’lmagan ma’lum bir bal qo’shilib boradi. Bu onlayn hakamda foydalanuvchilar reytingi ularning yig’gan ballariga bog’liq, ya’ni eng yuqori bal olgan foydalanuvchi 1-o’rin, eng kam bal yig’gan foydalanuvchi oxirgi o’rinda turadi, bir xil bal yig’gan foydalanuvchilar esa bir xil o’rinda bo’lishadi. Masalan jami 4 ta foydalanuvchi bo’lsa va ularning yig’gan ballari [100, 90, 90, 80] bo’ladigan bo’lsa, bu foydalanuvchilarning tizimdagi joriy reytingi [1, 2, 2, 3] kabi bo’ladi.
Megaboy BaytContest tizimida ro’yxatdan o’tganidan so’ng jami M ta masalani ishlab bo’lganiga qadar tizimdan undan boshqa hech bir foydalanuvchi foydalanmagani ma’lum.
Birinchi satrda bitta butun son, N(1 ≤ N ≤ 2×105) – tizimdagi megaboydan tashqari foydalanuvchilar soni, ikkinchi satrda N ta butun son, har bir foydalanuvchining tizimda yig’gan bali (reyting boshidan toki oxiriga qadar), uchinchi satrda bitta butun son, M(1 ≤ M ≤ 2×105) – Megaboy ishlagan masalalar soni, to’rtinchi qatorda M ta butun son, Megaboyning har bir masalani ishlaganidan keyingi umumiy bali kiritiladi. Barcha kiritilgan ballar [0, 109] orasida ekanligi kafolotlanadi.
Megaboyning har bir masalani ishlagandan keyingi tizimdagi reytingini alohida qatorda chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
7 100 100 50 40 40 20 10 4 5 25 50 120 |
6 4 2 1 |
C. Shaxmat musobaqasi
Xotira: 16 MB, Vaqt: 1000 msBaytlandiya mamlakatida shaxmat o’yinchilar jami 100 ta darajaga bo’lingan, 1-darajali shaxmat o’yinchisi strategik jihatdan eng kuchsiz hisoblanadi, 100-darajali shaxmat o’yinchisi esa strategik jihatdan eng kuchli hisoblanadi. Va yanam shu ma’lumki, bu mamlakatda strategik kuchli o’yinchi doim shaxmat musobaqasida strategik kuchsizroq o’yinchining ustidan g’alaba qozongan, strategiyasi tenglar esa o’yinda teng kuchli bo’lib doim during natija qayd etishgan. Bu mamlakatda shunday kitob borki, uni 1 marotaba o’qigan shaxmatchining strategiyasi 1 ga ortadi, bu kitobni bir necha marotaba o’qib chiqish mumkin, va har o’qiganda strategik darajasi 1 ga ortib boraveradi (100-darajaga yetgandan so’ng strategik daraja ortmaydi).
Megaboy xalqaro shaxmat musobaqasining saralash bosqichiga qatnashmoqchi, hozirda uning strategik darajasi k ga teng. Boshqa ishtirokchilardan farqli o’laroq Megaboy shaxmat musobaqasi tashkilotchisining o’g’li va u otasining yordamida o’z raqiblarining strategik kuchlilik darajalarini aniqlab oldi. Uning aniqlashicha musobaqa jarayonida unga jami N ta raqib to’g’ri keladi. O’yinda keyingi bosqichga faqatgina hech kimga yutqazmagan o’yinchilargina chiqa oladi. Siz Megaboy keyingi bosqichga o’ta olishi uchun shaxmatchilar kitobini eng kamida necha marotaba o’qib chiqishi kerakligini aniqlang.
Dastlabki satrda ikkita butun son, N(1 ≤ N ≤ 100) va K sonlari kiritiladi. Keyingi qatorda N ta butun son, Megaboyning raqiblarining strategik darajalari kiritiladi.
Megaboy keyingi bosqichga o’ta olishi uchun shaxmatchilar kitobini eng kamida necha marotaba o’qib chiqishi kerakligini aniqlang.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 4 1 6 3 5 2 |
2 |
D. O’rmon
Xotira: 16 MB, Vaqt: 1000 msSizga o’rmon berilgan (oddiy bog’lanishlardan iborat, sikl mavjud bo’lmagan graf).
Har bir daraxtda tugunlar soni juft bo’ladigan qilib o’rmondan maksimal sondagi qirralarni olib tashlang.
Misol uchun tugunlar soni 4 bo’lgan quyidagi daraxtdan 1 ta qirrani olib tashlash mumkin:
Dastlabki satrda ikkita butun son, N va M (0 < M < N ≤ 100) – o’rmondagi barcha daraxtlarning jami tugunlar soni va jami qirralar soni. Keyingi M ta qatorda har bir qirra bog’lab turgan tugunlar juftligi kiritiladi.
Har bir daraxtda tugunlar soni juft bo’ladigan qilib o’rmondan maksimal nechta qirrani olib tashlash mumkinligini chop eting. Yechim mavjudligi kafolotlanadi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
10 9 2 1 3 1 4 3 5 2 6 1 7 2 8 6 9 8 10 8 |
2 |
E. Adizning birlashtirish algoritmi
Xotira: 32 MB, Vaqt: 2000 msLaziz Adizga V massivlar to’plamini M massivga birlashtirish uchun berdi. Adiz massivlarni shunchaki ketma-ket birlashtirishni xoxlamay, o’zi massivni birlashtirishning boshqacha usulini o’ylab topdi. Uning birlashtirish usuli quyidagicha:
-
M=[] bo’sh massivni yaratib oladi
-
k=V massivlar to’plamidagi massivlar soni
-
V to’plamda kamida 1 ta bo’sh bo’lmagan massiv mavjud bo’lsa
-
T = [] bo’sh massivni oladi
-
i = 1
-
i <= k shart qanoatlansa
-
agar Vi bo’sh bo’lmasa
-
Vi ning birinchi elementini o’chirib, uni T massivga qo’shadi
-
-
i = i + 1
-
-
T bo’sh bo’lib qolmaguniga qadar
-
T dan eng kichik elementni o’chirib M ning davomidan qo’shadi
-
-
-
M ni chop etadi
Quyidagi misolda ko’ramiz: V={[3, 5], [1], [2, 4]} bo’lsin
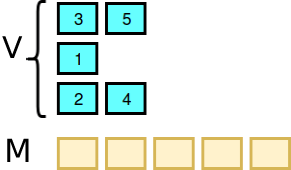
Shunda Adiz quyidagicha amallar ketma-ketligini bajaradi:
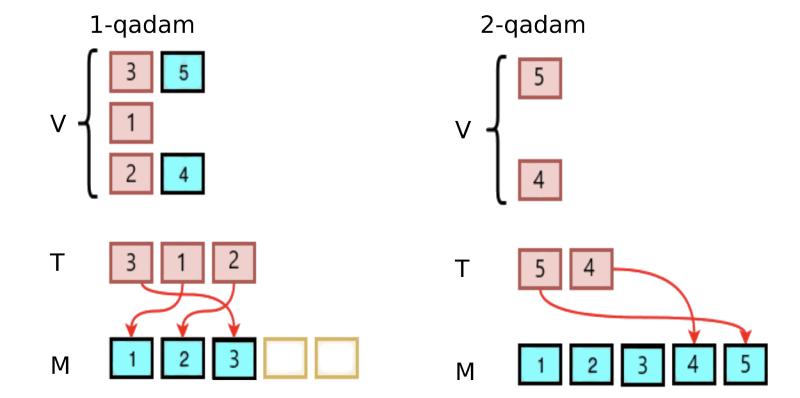
Laziz o’zidagi V massivlar to’plamini Adizga berganidan so’ng Adiz o’zining birlashtirish algoritmi orqali massivlarni birlashtirib hosil bo’lgan M massivni Lazizga berdi. Bir necha kundan so’ng Laziz o’zidagi V massivlar to’plamini yo’qotib qo’ydi, unda hozir Adiz birlashtirib bergan M massiv bor xolos. Endi u o’zining V to’plamini qayta tiklamoqchi.
Birinchi satrda bitta butun son, N(1 <= N <= 1200), keyingi satrda N ta butun son, M(1 <= Mi <= N) massiv elementlari kiritiladi.
Laziz o’zining V massivlar to’plamini necha xil ko’rinishda qayta tiklashi mumkinligini aniqlang. Bu son juda katta bo’lishi mumkin, siz shu sonning 109+7 ga bo’lgandagi qiymatini chop eting.
|
1-test |
||||||||||||||
|
1-usul |
|
2-usul |
|
3-usul |
|
4-usul |
||||||||
|
1 |
2 |
3 |
|
1 |
3 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-test |
||||||||||||||
|
1-usul |
|
2-usul |
|
3-usul |
|
|
|
|
||||||
|
2 |
3 |
1 |
|
2 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
1 |
|
|
|
|
|
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 1 2 3 |
4 |
| 2 |
3 2 3 1 |
3 |