A. Nokia

Xotira: 16 MB, Vaqt: 1000 ms
Masala

Abdulla aqlli telefonlarni ishlatishni yoqtirmaydi. U yaqinda Nokia 6300 rusumidagi telefon sotib oldi. Abdullaga telefon juda ham maqul kelgan edi, lekin bir muammo ham bor edi, bu telefonda sms yozish bir munchagina qiyinchilik tug’dirar edi. 

Abdulla \(S\) satrni do’stiga sms qilib jo’natmoqchi bo’ldi va u necha marta klaviatura bosishiga qiziqib qoldi. \(S\) satrda faqat kichik lotin harflari va bo’shliq (probel) belgilari mavjud. Lotin alifbosi telefon klaviaturasiga qanday joylashganligini quyidagi rasm orqali bilib olish mumkin.

Klaviaturada bo’shliq (probel) 0 ga joylashtirilgan. 0 ni bir marotaba bosish orqali  bo’shliq (probel) qo’yiladi. 

Misol uchun, ushbu telefon orqali \(\text{“salom”}\) so’zini yozish uchun 12 marta klaviaturani bosish talab qilinadi. Bunga sabab \(\text{“s”}\) belgisi uchun 7-klaviatura 4 marta, \(\text{“a”}\) belgisi uchun 2-klaviatura 1 marta, \(\text{“l”}\) belgisi uchun 5-klaviatura 3 marta, \(\text{“o”}\) belgisi uchun 6-klaviatura 3 marta va \(\text{“m”}\) belgisi uchun 6-klaviatura 1 marta bosiladi.

 

https://robocontest.uz/storage/images/309.jpg 

Kiruvchi ma'lumotlar:

Bitta satrda faqat kichik lotin harflari va bo’shliq (probel)dan iborat matn. Matn uzunligi 100 000 dan oshmaydi.

Chiquvchi ma'lumotlar:

Berilgan matnni yozish uchun eng kamida necha marta klaviatura bosilishini chop eting.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
salom
 
12
2 
yosh dasturchilar musobaqasiga xush kelibsiz
 
101

B. Fraktal

Xotira: 16 MB, Vaqt: 1000 ms
Masala

Asadullo fraktal shakllarga qiziqadi. U yangi fraktal shakl o’ylab topdi va uni quyidagi tartibda to’ldira boshladi:

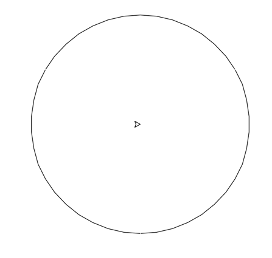
  • 1-qadamda Asadullo \(R\) radiusli aylana chizib oldi.
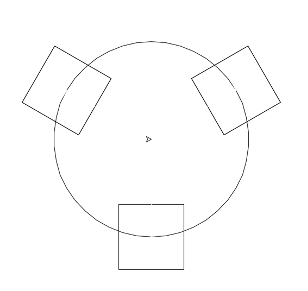
  • 2-qadamda 1-qadamda chizilgan aylananing atrofida 3 ta kvadrat chizdi
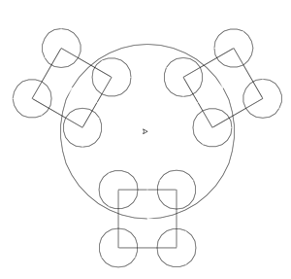
  • 3-qadamda 2-qadamda chizilgan kvadratlarning to’rttala qirrasida ham aylana chizdi
  • …
  • \(2*k\) – qadamda \(2*k-1\) – qadamda chizilgan aylanalarning atrofida 3 tadan kvadrat chizdi
  • \(2*k+1\) – qadamda \(2*k\) – qadamda chizilgan kvadratlarning to’rttala qirrasida ham aylana chizdi
  • …

1-bosqich

2-bosqich

3-bosqich

 

Asadullo ushbu fraktal shaklning \(N\)-qadamigacha chizib chiqish murakkab ekanligini, lekin, \(N\)-qadamgacha jami nechta shakl chizilganini (aylana va kvadratlar) aniqlash mumkinligini  tushunib yetdi. Asadulloga \(N\)-qadamgacha chizilgan shakllar sonini aniqlashda yordam bering.

Kiruvchi ma'lumotlar:

Kirish faylida yagona butun son, \(N(1 ≤ N ≤ 10^{18)}\) soni kiritiladi.

Chiquvchi ma'lumotlar:

Chiqish faylida yagona son, \(N\)-qadamigacha chizilgan shakllar umumiy sonini \(1000000007(10^9+7)\) ga bo’lgandagi qoldiqni chop eting!

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
1
 
1
2 
2
 
4
3 
3
 
16

C. Juft raqamli natural son

Xotira: 16 MB, Vaqt: 1000 ms
Masala

Yozilishida kamida bitta juft raqam bo'lgan \(N\)-natural sonni aniqlang!

Kiruvchi ma'lumotlar:

Kirish faylida yagona natural son, \(N (1 ≤ N ≤ 10^{18})\) soni kiritiladi

Chiquvchi ma'lumotlar:

Chiqish faylida yagona son, yozilishida kamida bitta juft raqam bo'lgan \(N\)-natural sonni chop eting!

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
5
 
10
2 
10
 
20
3 
20
 
30

D. Nuqtalar

Xotira: 16 MB, Vaqt: 1000 ms
Masala

\(Ox\) o’qida joylashgan \(n\) ta nuqta berilgan. Ular mos ravishda \(x_1, x_2, …, x_n\) koordinatalarda joylashgan. Sizning vazifangiz berilgan \(n\) ta nuqtani bir chiziqda ketma-ket joylashtirish uchun minimal qancha amal ketishini topishdan iborat. Ya’ni bir chiziqqa qo’yganingizdan so’ng, eng chapdagi nuqta koordinatasi \(x\) bo’lsa, keying nuqta koordinatalari mos ravishda \(x+1, x+2,…,x+n‑1\) bo’lishi lozim.

Bir amalda ixtiyoriy nuqtani bir marta o’ngga yoki chapga surish mumkin.

Kiruvchi ma'lumotlar:

Birinchi qatorda bitta butun \(n(n ≤ 10^5)\) soni . Keyingi qatorda esa \(n\) ta  butun son \(x_1, x_2, …, x_n(x_i ≤ 10^9)\).

Chiquvchi ma'lumotlar:

Chiqish faylida bitta butun son – minimal amallar sonini chiqaring.

Izoh:

Tushuntirish. Nuqtalarni \(1, 2, 3, 4, 5\) - o'rinlarga yig'amiz. Buning uchun:
1- nuqta 1-koordinatada qoladi
2-nuqta 5-koordinataga ko'chiriladi, buning uchun \(|9-5|=4\) ta amal kerak
3-nuqta 2-koordinataga ko'chiriladi, buning uchun 1 ta amal kerak
4-nuqta 4-koordinataga ko'chiriladi, buning uchun \(|6-4| = 2\) ta amal kerak
5-nuqta 3-koordinataga ko'chiriladi, buning uchun \(|3-2| = 1\) ta amal kerak
Shunday qilib jami amallar soni \(0+4+1+2+1 = 8\)

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
5
1 9 1 6 2
 
8
Kitob yaratilingan sana: 22-Nov-24 21:41