A. Uchburchak

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Siz bu masalada, sizga berilgan 3ta kesmadan foydalanib, uchburchak yasash mumkinmi yoki yo'qmi shuni tekshirishingiz kerak. Agar 3ta kesma hosil qilgan uchburchak, teng tomonli bo'lsa, “Teng tomonli”, agar teng yonli bo'lsa, “Teng yonli”, agar turli tomonli bo'lsa, “Turli tomonli” deb (qo'shtirnoqlarsiz) chop eting. Agar bu 3ta kesmadan uchburchak hosil qilib bo'lmasa, “NO” deb chop eting.

Kiruvchi ma'lumotlar:

Bitta qatorda 3ta natural son a, b, c - har bir kesma uzunliklari bo'sh joy bilan ajratilgan holda kiritiladi. \(1\leq a, b, c \leq 10^9\)

Chiquvchi ma'lumotlar:

Uchburchak turi yoki “NO” chop eting.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1 2 2	Teng yonli
2	1 1 1	Teng tomonli
3	3 3 7	NO

B. Ali va Vali

Xotira: 256 MB, Vaqt: 750 ms

Masala

Bir kuni Ali bilan Vali o'yin o'ynashmoqchi bo'lishibdi. O'yinda ularga \(s\) binar satr beriladi. Dastlab, berilgan faqat 0 va 1 lardan iborat \(s\) binar satri o'nlik sanoq sistemasiga o'tkaziladi, o'girilgan sonni \(n\) deb olaylik. Ali va Vali bu \(n\) soni ustida quyidagi amallarni o'yin tugagunicha bajarishadi:

Agar \(n\) soni toq bo'lsa, Ali unga 1ni qo'shadi. n \(\leftarrow\) n + 1

Agar \(n\) soni juft bo'lsa, Vali uni 2ga bo'ladi. \(n\leftarrow \frac{n}{2}\)

O'yin \(n\) soni 1ga teng bo'lgunicha davom etadi, ya'ni \(n=1\)da o'yin tugaydi. Siz Ali va Valining har biri nechtadan amal bajaranligini toping. \(s\) satrining dastlabki raqami 0dan farqli bo'lishi kafolatlanadi.

Kiruvchi ma'lumotlar:

Yagona qatorda \(s\) binar satri beriladi. \(1 \leq |s| \leq 10^6\)

Chiquvchi ma'lumotlar:

Ali va Vali nechtadan amal bajarganligini chop eting. Birinchi Ali, keyin esa Vali.

Izoh:

\(11_2 = 3_{10}\). n toqligi sabab, Ali 1ni qo'shadi: \(n=3+1=4\).

Endi esa, Vali sonni ikki marta ikkiga bo'ladi: \(n = \frac{4}{2}\),

\(n = \frac{2}{2} = 1\).

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	11	1 2
2	100	0 2

C. Dynamoning o'yini

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Sonlarni sanashni tezda o'rganib olgan 1-sinf o'quvchisi Dynamo, hozir ularni yozishni o'rganyapti. 1-sinflarning eng a'lochi o'quvchisi sifatida u 1dan 4gacha sonlarni sanashni va yozishni o'rgandi. Lekin, u 4 soni 1 sonining boshqacha yozilishi deb o'ylaydi. Kunlardan bir kun, u o'ziga-o'zi o'yin yaratdi. Dastlab, u o'zi istagan sonni yozadi va uning raqamlari qo'shib chiqadi. (u istalgan sonni yozishda faqatgina o'zi bilgan raqamlardan foydalanadi). Masalan, 423 sonini olaylik, \(1+2+3=6\) (u 4sonini 1 bilan bir xil deb o'ylaydi). 1223 sonini oladigan bo'lsak, \(1+2+2+3=8\). Dynamo bu o'yinni ancha vaqtdan beri o'ynab kelyapti, lekin endi, u raqamlari yig'indisi \(n\) ga teng bo'lgan sonlar nechtaligiga qiziqib qoldi.

Kiruvchi ma'lumotlar:

Kirish faylida bitta natural \(n\) soni beriladi. \(1\leq n\leq 10^6\)

Chiquvchi ma'lumotlar:

Dynamo yoza oladigan va raqamlari yig'indisi (raqamlari yig'indisi Dynamoning o'yini bo'yicha hisoblanadi) \(n\) ga teng bo'lgan sonlar sonini chop eting. Natija katta bo'lganligi bois, javobni \(10^9+7\)ga bo'lgandagi qoldiqni chop eting.

Izoh:

\(n=1\) bo'lganda, u tuza oladigan va raqamlari yig'indisi 1ga teng bo'lgan sonlar, 2ta: 1 va 4.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3	13
2	6	214

D. Reverse in range

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Sizga \(S\) satri va \(Q\) ta son beriladi. \(S\) satri ustida \(Q\) marotaba amal bajarasiz. Har bir \(Q_i\) son uchun \(S\) satrining boshidan va oxiridan \(Q_i -1\) ta harfni olib tashlangandan so'ng hosil bo'lgan substring ni teskarisiga o'girilgan holatda joyiga qaytarasiz. \(Q_{i+1}\) uchun esa o'zgargan satrdan foydalanasiz.

Kiruvchi ma'lumotlar:

Birinchi qatorda \(S\) satri beriladi.

Ikkinchi qatorda \(Q\) soni, va keyingi qatorda \(Q\) ta butun son beriladi.

\(1 \leq |S| \leq 10^5\)
\(1 \leq Q \leq 10^5\)
\(1 \leq Q_i \leq \left \lfloor \frac{|S|}{2} \right \rfloor\)

Chiquvchi ma'lumotlar:

Yagona satrda masala javobi, hosil bo'lgan satrni chop eting.

Izoh:

Testlar misollardagidan farq qilishi mumkin!

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	robocontest 1 2	rsetnocobot
2	robocontest 2 2 4	rseocontbot

E. Yangi tetris

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Hammamiz ham yoshligimizda tetris o'yinini o'ynagan bo'lsak kerak. Lekin, bu masaladagi tetris o'yini boshqa tetrislardan keskin farq qiladi.

• Bu o'yinda faqat 2 turdagi to'g'ri to'rtburchaklardan foydalanish mumkin:

eni \(1\) ga va bo'yi istalgan qiymatga teng to'g'ri to'rtburchak.
bo'yi \(1\) ga va eni istalgan qiymatga teng to'g'ri to'rtburchak

• Bitta katakka 2ta to'g'ri to'rtburchakni ustma-ust joylashtirsa bo'ladi.

• Qator gorizontaliga to'lganda, u yo'q bo'lib ketmaydi.

O'yinchining vazifasi ko'proq o'yin o'ynash emas, balki eng kam to'g'ri to'rtburchaklar yordamida, berilgan shaklni yasash.

Kiruvchi ma'lumotlar:

Birinchi qatorda \(n\) soni - shakldagi ustunlar soni. Keyingi qatorda \(a_{i}\) - shaklning \(i\) ustunining balandligi.

\(1\leq n\leq 2*10^3\)

\(1\leq a_i\leq 10^9\)

Chiquvchi ma'lumotlar:

Shaklni yasash uchun minimum nechta to'g'ri to'rtburchak kerakligini chop eting.

Izoh:

1 va 2-test uchun izoh:

Misollar:

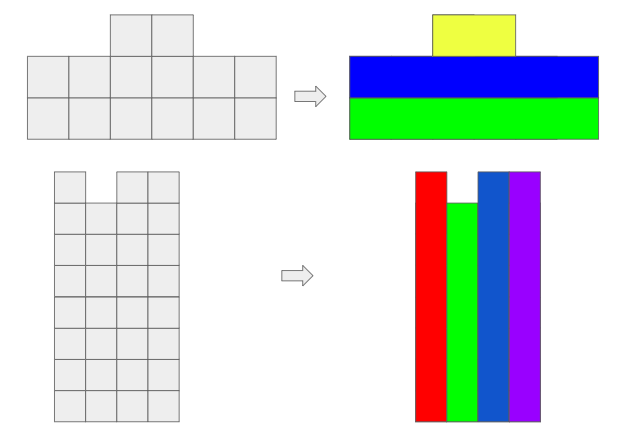
#	INPUT.TXT	OUTPUT.TXT
1	6 2 2 3 3 2 2	3
2	4 8 7 8 8	4

F. Change Binary strings

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Sizga bir xil uzunlikdagi \(S\) va \(T\) satrlari beriladi. Ular faqat \(a\) va \(b\) dan tashkil topgan. Sizda \(S\) satriga o'zgartirish kiritish uchun 2ta yo'l bor.

Istalgan \(x\) sonini tanlaysiz (\(0\leq x < |S|\)) va agar \(S_x\) \(a\) bo'lsa \(b\) ga, \(b\) bo'lsa esa \(a\) ga o'zgartirasiz.
Istalgan ikkita son, \(x\) va \(y\) sonlarini tanlaysiz (\(0\leq x, y < |S|\)) va \(S_x\) va \(S_y\) ni almashtirasiz.

Birinchi yo'l uchun sizdan 1 tanga, ikkinchi yo'l uchun esa \(|y-x|\) tanga olinadi. Siz esa S va T satrlarini tenglash uchun ketadigan minimal tangalar sonini toping!

Kiruvchi ma'lumotlar:

Birinchi qatorda N, S satrning uzunligi kiritiladi.

Keyingi qatorda S satri, 3-qatorda esa T satri beriladi.

\(1 \leq N \leq 10^6\)
\(|S| = |T| = N\)

Chiquvchi ma'lumotlar:

Yagona qatorda masala javobini chop eting!

Izoh:

1-testga izoh:

s = ‘aab’, t = ‘baa’;

s satrning oxirgi harfi \(b\) ni \(a\) harfiga o'zgartiramiz. +1 tanga. s = ‘aaa’;

s satrning birinchi harfi \(a\) ni \(b\) harfiga o'zgartiramiz. +1 tanga. s = ‘baa’;

s = t; #tangalar = 2;

Boshqa yo'li esa \(x=0, y=2\) holatda \(swap(s_x, ~ s_y)\) qilsak, s = t holatga keladi. #tangalar = 2;

Testlar misollardagidan farq qilishi mumkin!

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 aab baa	2
2	4 abab aabb	1

G. Mukammal jadval

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Sizda tomoni \(N\) ga teng bo’lgan jadval bor. Siz esa bu jadvaldan ‘Mukammal’ jadvalni hosil qiling. ‘Mukammal’ jadval bo’lishi uchun 2ta shart bor:
• Uning 4 tomonining uzunligi ham \(N\) ga teng bo'lishi kerak
• Uning har bir katagida \(1\) yoki \(0\) yozilishi shart

Ikki jadvalning har xilligi deb, shu ikki jadval bir-biridan, birini qanchadir gradusga aylantirganda ikkinchisi bilan bir xil bo’lib qolmasligiga aytiladi.
Sizning vazifangiz shundan iboratki, bu \(N\times N\) jadvaldan hosil qilish mumkin bo’lgan har xil ‘Mukammal’ jadvallar sonini toping.

Kiruvchi ma'lumotlar:

Kirish faylida, bitta butun son N (\(1\leq N\leq10^9\)) beriladi.

Chiquvchi ma'lumotlar:

Tomoni \(N\) ga teng bo'lgan ‘Mukammal’ jadvallar sonini toping. Bunday jadvallar soni juda katta bo'lib ketishi mumkin, shuning uchun javobni \(10^9+7\)ga bo'lgandagi qoldiqni chop eting.

Izoh:

\(N=2\) bo'lganda hosil qilib bo'ladigan mukammal jadvallar:

Misollar:

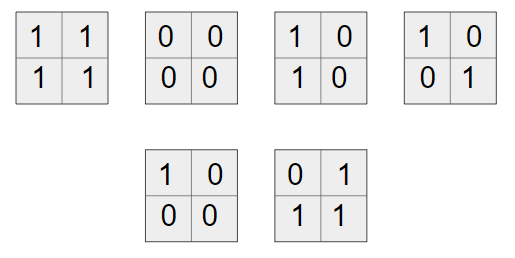
#	INPUT.TXT	OUTPUT.TXT
1	2	6
2	5	8390720
3	9	5179184

H. Maximal Qiymat

Xotira: 64 MB, Vaqt: 1000 ms

Masala

Tasavvur qiling, siz RoboLand kompaniyasi boshlig'isiz. Bugun bu kompaniyangiz yong'in ostida. Siz bu kompaniyangizni turli xonalarida qimmatbaho(olovda yonuvchi) taqinchoqlar saqlaysiz. Bu taqinchoqlar soni \(N\)ta bo'lib, har birining siz uchun alohida o'rni bor, ya'ni \(i-\)taqinchoq siz uchun \(v_i\) qiymatga ega. Siz bu xonalarning uzoqligini inobatga olgan xolda, \(i-\) xonaga borish uchun \(T_i\) vaqt ketishini bilib oldingiz. Yong'in boshlangandan \(S_i\) vaqt o'tib \(i-\)xona yonib bitadi. Sizning vazifangiz, iloji boricha ko'p qiymatli taqinchoqlarni saqlab qolishdan iborat!!!

!!! Diqqat !!! \(T_i\geq S_i\) holatda siz \(i-\)taqinchoqni saqlashga ulgura olmaysiz)

Kiruvchi ma'lumotlar:

Birinchi qatorda \(N\) soni kiritiladi.

Keyingi \(N\)ta qatorda mos ravishda \(T_i, ~S_i\) va \(v_i\) sonlari beriladi.

\(1 \leq N \leq 2*10^3\)
\(1 \leq T_i \leq 20\)
\(1 \leq S_i \leq 2 * 10^3\)
\(1 \leq v_i \leq 10^9\)

Chiquvchi ma'lumotlar:

Yagona qatorda, siz saqlab qolishingiz bo'lgan maksimal qiymatlar yig'indisini chop eting!

Izoh:

1-testga Izoh:

Siz istalgan 2ta taqinchoqni saqlab qola olasiz, Masalan: Birinchi bo'lib 3-taqinchoqni saqlab qolamiz. So'ng hozirgi vaqt 3ga teng bo'ladi. Keyin esa birinchi taqinchoqni olamiz va 6-unit vaqtda u xonadan chiqamiz. Ammo, biz ikkinchi taqinchoqqa endi ulgurmaymiz. Demak hozir bizda 6 + 4 = 10 qiymatga ega taqinchoqlar saqlab qolindi. Ammo bu optimal yo'l emas.

Optimal yo'l:

Birinchi bo'lib 2-taqinchoqni olib, so'ng 3-taqinchoqga o'tamiz. 1-taqinchoqqa borgunimizcha esa vaqt 8-unitda bo'ladi, demak bora olmaymiz. Bizdagi qiymat 6 + 5 = 11;

Ikkinchi test uchun optimal yo'l:

Ikkinchi xonaga borganimiz zahoti xona yonadi. Shuning uchun birinchi bo'lib birinchi xonaga yo'l olamiz va taqinchoqni olishga ulguramiz. Javob 1;

Testlar misollardagidan farq qilishi mumkin!

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 3 7 4	11
2	2 5 6 1	1