A. Ko’pburchaklarni bo’lish

Xotira: 64 MB, Vaqt: 1000 ms
Masala

Sizga N burchakli muntazam ko’pburchak berilgan, siz unga N – 3 ta kesishmaydigan dioganallar o’tkazishingiz kerak. Sizning vazifangiz bu dioganallarni necha xil usulda o’tkazish mumkin ekanligini aniqlashdan iborat. Bu son juda katta bo’lib ketishi mumkin shuning uchun qiymatini 1000000007 ga bo’lgandagi qoldiqni javob sifatida chiqarishingiz so’ralyapti.

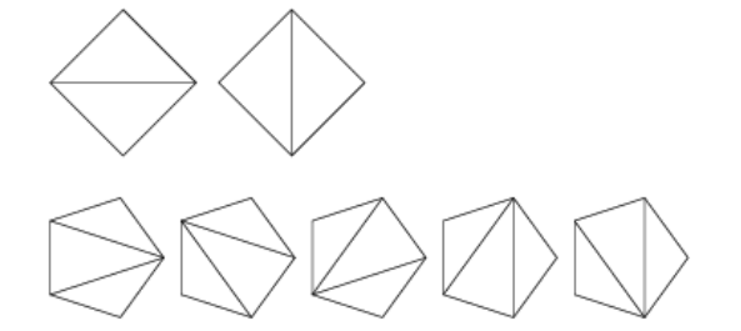
Yuqorida berilgan rasmda 4 va 5 burchakli muntazam ko’pburchaklar uchun natijalar ko’rsatilgan.

Kiruvchi ma'lumotlar:

Bitta qatorda N soni beriladi \(( 3 < N < 1000)\)

Chiquvchi ma'lumotlar:

Masalaning javobini \(1000000007\) ga bo’lgandagi qoldiqni toping

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
4
 
2
2 
5
 
5

B. Habibulloh o’ylagan ketma ketlik

Xotira: 64 MB, Vaqt: 1000 ms
Masala

Habibulloh har xil ketma-ketliklarni yaxshi ko’rardi, u kunlardan bir kun bir‑biriga bog’liq bo’lgan ketma-ketlikni o’ylab topdi. Uning o’ylab topgan ketma‑ketligi quyidagicha.

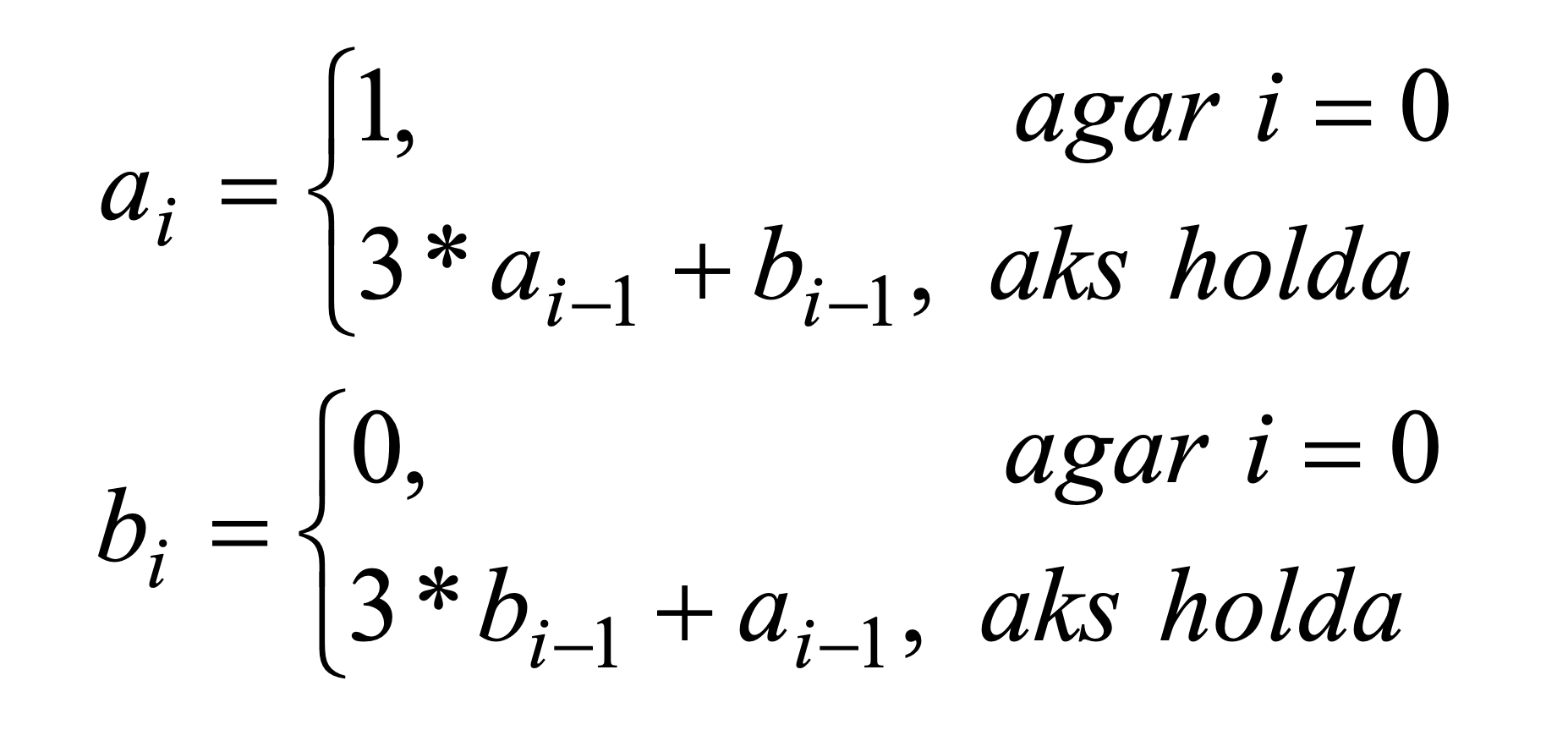
Habibulloh bu ketma – ketlikning n chi hadidagi a ning qiymatini bilmoqchi, Unga buni hisoblashda yordam bering.

Kiruvchi ma'lumotlar:

Bitta qatorda \(n ( 0 \le n \le 10^{18})\) butun son

Chiquvchi ma'lumotlar:

\(a_n\) ning qiymatini \(10^9+7\) ga bo’lgandagi qoldiqni chiqaring

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
1
 
3
2 
2
 
10
3 
3
 
36

C. Aslbekning piramidasi

Xotira: 64 MB, Vaqt: 1000 ms
Masala

Aslbek piramidalarga juda qiziqadi. U bir kuni kubiklardan piramida qurish haqida o’ylab qoldi. U mumkin qadar kam kubiklardan maksimal balandlikdagi piramidani qurishni o’ylardi. Bu piramidani qurish uchun kubiklarni joylashtirishga quyidagi shartlarni qo’ydi.

Valid

Invalid

 

U piramidaning mustahkamligi haqida ham o’yladi va mustahkamlikni ta’minlash uchun quyidagicha shartlar qo’ydi.

Mustahkam

Mustahkam emas

Endi u N qavatli piramida qurish uchun nechta kubik sotib olishi kerakligi haqida o’ylayapti.

Kiruvchi ma'lumotlar:

Birinchi qatorda bitta butun son \(N (1≤N≤10^9)\) qavatlar soni berilgan.

Chiquvchi ma'lumotlar:

N qavatli piramida qurish uchun kerak bo’lgan kubiklar sonini \(10^9+7\) ga bo’lgandagi qoldiqni ekranga chiqaring.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
1
 
1
2 
2
 
6

D. To’g’ri to’rtburchakdagi romblar

Xotira: 64 MB, Vaqt: 1000 ms
Masala

         Aslbek matematika darsida katakli daftarga to’g’ri to’rtburchak chizdi va bu to’g’ri to’rtburchak ichiga nechta romb chiza olishi to’g’risida o’ylab qoldi. Agar uchlarni haqiqiy qiymatli nuqtalarda joylashtirsa, bunday ko’pburchaklar cheksiz ko’p bo’lishini bilganligi uchun quyidagi shartlarni kiritib oldi.

  • Musbat yuzaga ega bo’lsin
  • Romb uchlari butun buqtalarda yotsin
  • Rombning barcha uchlari shu to’g’ri to’rtburchak ichida yotsin
  • Diagonallari koordinata o’qlariga parallel bo’lsin

Aslbekka bu shartlarni bajaradigan romblarning sonini topishda yordam bering

Kiruvchi ma'lumotlar:

Birinchi qatorda ikkita butun sonlar \(x_1 (-10^4≤x_1≤10^4)\), \(y_1(-10^4 ≤ y_1 ≤ 10^4)\) to’g’ri to’rtburchakning birinchi uchi, ikkinchi qatorda ham ikkita butun sonlar \(x_2 (-10^4≤x_2≤10^4)\), \(y_2(-10^4≤y_2≤10^4)\) to’g’ri to’rtburchakning ikkinchi uchi

Chiquvchi ma'lumotlar:

Yuqoridagi shartlarni bajaruvchi romblar sonini chiqaring

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
0 0
2 2

1
2 
0 1
1 0

0

E. Matematik Mod

Xotira: 256 MB, Vaqt: 1000 ms
Masala

Quvonchbeka ustozi Matematika darsida 2 ta soni qoldiq olib berishini soradi, Afsuski Quvonchbek bu haqida bilmas edi .Sizga unga yordam bering . Quvonchbeka ustozi ikkita butun son berilgan \(l\) va \(r, l≤ r\)  Shu oraliqda mumkin bolgan \(( a , b )\) shunday olinki a mod b eng kata bolsin \(r ≥ a ≥ b ≥ 1\).

Kiruvchi ma'lumotlar:

Birinchi qatorda bitta musbat \(t (1≤t≤10^4)\) testlar soni kiritiladi.

Har bir testninng 1-qatorda ikkita \(l, r (1≤l≤r≤10^9)\) butun sonilar kiritiladi.

Chiquvchi ma'lumotlar:

Har bir test uchun \(r≥a≥b≥l\) boʻlgan barcha juftlik \((a, b)\) butun sonlar ustiga \(a \space \text{mod} \space b\) ning qiymati bolishi mumkin bolgan eng katta qiymatini chop eting.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
4
1 1
999999999 1000000000
8 26
1 999999999
 
0
1
12
499999999

F. Matrisadan izlash

Xotira: 256 MB, Vaqt: 1000 ms
Masala

\(N\) ta satr va \(n\) ta ustundan iborat jadvalni korib chiqaylik. Malumki \(i\)-qator va \(j\)-ustuning kesishmasidan hosil bolgan katakchada \(i \times j\) sonlar mavjud. Qator va ustunlar 1 dan boshlab raqamlanadi.

\(X\) musbat butun son beriladi. Jadvalda nechta \(x\) joylashgan katakcha borligini sanang.

Kiruvchi ma'lumotlar:

Yagona qatorda \(n\) va \(x(1 \le n \le 10^5, 1 \le x \le 10^9)\) kiritiladi.

Chiquvchi ma'lumotlar:

X soni jadvalda necha marta uchraganini chop eting.

Izoh:

1 - Test

1

2

3

4

5

6

2

4

6

8

10

12

3

6

9

12

15

18

4

8

12

16

20

24

5

10

15

20

25

30

6

12

18

24

30

36
Misollar:
# INPUT.TXT OUTPUT.TXT
1 
6 12
 
4

G. Matematika haqida

Xotira: 16 MB, Vaqt: 1000 ms
Masala

Hisob kitob ishlarida yangi muammoni hal qilish usullaridan biri - matematikadan foydalanishdir. Misol uchun, siz biron bir Piramida yuzini topish uchun teorema lardan foydalanasiz. Bunaqa teoremalar juda ham kop.

Masalan, Goldbax gipotezasida: "Har qanday juft son ikkita kompozit sonning yig'indisi shaklida ifodalash mumkin". Uni ozgina ozgartiramiz yani: "12 dan katta bo'lgan har bir butun sonni ikkita kompozit sonning yig'indisi shaklida ifodalash mumkin." Goldbaxning taxminidan farqli o'laroq, men bu taxminni isbotlay olaman.

Kiruvchi ma'lumotlar:

Yagona qatorda \(n (12 ≤  n  ≤ 1000000)\) butun son kiritiladi.

Chiquvchi ma'lumotlar:

\(x\) va \(y (1 <  x ,  y  <  n )\) ikkita kompozit butun sonlarni yig'indisi shaklida tasvirlang \((x  +  y  =  n)\). Agar bir nechta to'g'ri javoblar bo'lsa, ulardan istalganini chop etishingiz mumkin.

Izoh:

Kompozit son - birdan katta ikkita natural sonning ko'paytmasi natijasida olingan son. Kompozit sonlar qatori: 4, 6, 8, 9, 10, 12, 14, va hokazo. Bir qator qoʻshma sonlar bitta xususiyatga ega – barcha kompozit raqamlar 2 yoki 3 ga boʻlinish qoldigʻisiz boʻlinadi.

1 – test, 12 = 4 + 8. 4 va 8 raqamlari yigindisi Shuningdek, siz "6 6" yoki "8 4" ni chiqarishingiz mumkin.

2 – test, 15 = 6 + 9. E'tibor bering, siz "1 14" ni chop eta olmaysiz, chunki 1 kompozit son emas.

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
12 
4 8

H. Eng katta umumiy bo'luvchi

Xotira: 16 MB, Vaqt: 2000 ms
Masala

Sizga n butun musbat soni beriladi.Siz \(a + b + c = n\) , \(\text{gcd}(a,b) = c\), \(b \ne c\) va \(a \ne c\) shartlarni qanoatlantiruvchi \(a,b,c\) sonlarni chop eting.
Bu yerda \(\text{gcd}(n,m)\) \(n\) va \(m\) sonini Eng katta umumiy bo'luvchidir.

Kiruvchi ma'lumotlar:

1-satrda testlar soni \(t(1 \le t \le 10^5)\) kiritiladi
Keyingi qatotlarda \(t\) ta \(n (10 \le n \le 10^9)\) kiritiladi

Chiquvchi ma'lumotlar:

Shartni qanoatlantiradigan \(a, b, c\) sonlarni 1 qatorda chop eting.Agar bunaqa sonlar bir nechtani tashkil qilsa istalganini chop eting.

Izoh:

1 - TEST: 6 + 9 + 3 = 18 va gcd (6, 9) = 3.
2 - TEST: 21 + 39 + 3 = 63 va gcd (21, 39) = 3.
3 - TEST: 29 + 43 + 1 = 73 va gcd (29, 43) = 1

Misollar:
# INPUT.TXT OUTPUT.TXT
1 
6
18
63
73
91
438
122690412

6 9 3
21 39 3
29 43 1
49 35 7
146 219 73
28622 122661788 2
Kitob yaratilingan sana: 25-Nov-24 13:02