Janob Alex Wice tomonidan tayyorlangan editorial. Buning uchun RoboContest.Uz jamoasi chuqur minnatdorchilik bildiramiz.
Shuningdek pastroqda RoboContest.Uz jamoasi yechimlari bilan tanishishingiz mumkin.
Q1 We have x * A + y * B <= M For every xA = 0, A, 2A, ... we find largest possible y * B This is y = (M - base) // B.
def solve(A, B, M):
ans = 0
for xA in range(0, M + 1, A):
y = (M - xA) // B
ans = max(ans, xA + y * B)
return ans
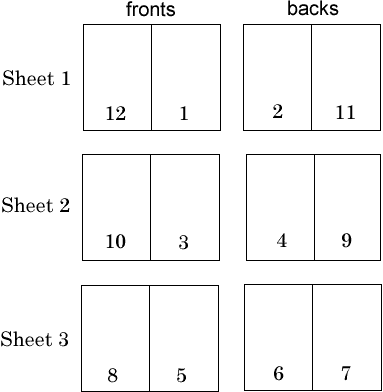
Q2 Each sheet is 4 pages, so the number of sheets is K = ceil(N / 4) Study this output carefully: 12 1 10 3 8 5 2 11 4 9 6 7 When looking at pairs of columns, the sheets can be arranged like this 12 1 2 11 10 3 4 9 8 5 6 7 of which the pattern can be derived.
def solve(N):
K = (N + 3) // 4
A = [0] * (2 * K)
B = [0] * (2 * K)
for x in range(2 * N):
if x % 2 == 0:
A[x + 1] = x + 1
else:
B[x + 1] = x + 1
for x in range(2 * N):
if x % 2 == 0:
B[2*K - 1 - x] = x + 2 * N + 1
else:
A[2*K - 1 - x] = x + 2 * N + 1
return K, A, B
Q3 Consider location (r, c) in the grid (0-indexed.) It's distances to the center is dr = abs(r - (N-1)), dc = abs(c - (N-1)) We care about min(dr, dc).
def solve(N):
M = 2 * N - 1
A = [[0] * M for _ in range(M)]
for r in range(M):
for c in range(M):
A[r][c] = min(abs(r - (N-1)), abs(c - (N-1))) + 1
return A
Q4 In the list A of divisors, max(A) must be one of the numbers. Say y = max(A). Now for every d dividing y, remove it from the list.
def solve(A):
y = max(A)
d = 1
while d * d <= y:
if y % d == 0:
A.remove(d)
if d * d != y:
A.remove(y // d)
d += 1
x = max(A)
return max(x, y), min(x, y)
Q5 Let odds(S) = the number of letters c with S.count(c) % 2 == 0. A string can be rearranged into a palindrome iff odds(S) <= 1. For characters that occur an even number of times, it doesn't affect the game, as odds(S) += 1 the first time (so it isn't a winning move) and the second player can just pick it again (odds(S) -= 1) which isn't worse. If odds(S) <= 1 at the beginning, it's a winning position. Otherwise, odds(S) % 2 dictates who wins.
def solve(A):
y = max(A)
d = 1
while d * d <= y:
if y % d == 0:
A.remove(d)
if d * d != y:
A.remove(y // d)
d += 1
x = max(A)
return max(x, y), min(x, y)
Q6 It suffices to answer which X in [1..N] are beautiful (ans = solve(R) - solve(L-1)) If K isn't a prime, the answer is 0. Now suppose K is prime. Multiples of K that are beautiful are either K or integers >= K * K. If K > 1e5, then only K is eligible (ans = 1 if N >= K else 0). Now suppose K <= 1e5. Naively, answer is ans = N // K, but we overcounted by multiples of p * K, so ans -= N // (p * K) for primes p < K. This undercounts by ans += N // (p * q * K) for primes p < q < K, and so on. We only need p1 * p2 * ... * p8 * K, since (p1 * ... * p9 * K) >= 6e9. This is fast in practice Alternative solution: you can PIE for K < 90, and you can brute force when K >= 90. (No code)
def solve(L, R, K):
return solve2(R, K) - solve(L-1, K)
def solve2(N, K):
if not is_prime(K): # implement this
return 0
if K > 1e5:
return +(N >= K)
P = list of primes < K # implement this
ans = N // K
for i1 in range(len(P)):
d1 = P[i1] * K
if d1 > N: break
ans -= N // d1
for i2 in range(i1 + 1, len(P)):
d2 = d1 * P[i2]
if d2 > N: break
ans += N // d2
for i3 in range(i2 + 1, len(P)):
d3 = d2 * P[i3]
if d3 > N: break
ans -= N // d3
for i4 in range(i3 + 1, len(P)):
d4 = d3 * P[i4]
if d4 > N: break
ans += N // d4
for i5 in range(i4 + 1, len(P)):
d5 = d4 * P[i5]
if d5 > N: break
ans -= N // d5
for i6 in range(i5 + 1, len(P)):
d6 = d5 * P[i6]
if d6 > N: break
ans += N // d6
for i7 in range(i6 + 1, len(P)):
d7 = d6 * P[i7]
if d7 > N: break
ans -= N // d7
for i8 in range(i7 + 1, len(P)):
d8 = d7 * P[i8]
ans += N // d8
return ans
Izoh: Bu masalani ishlash uchun shunchaki barcha holatlarni ko'rish yetarli bo'ladi. Ya'ni A idish bilan bo'lishi mumkin bo'lgan barcha holatlarni ko'rib chiqamiz va ulardan maksimalini javob sifatida olamiz.
Time Complexity-\(O(M/A)\)
Memory Complexity - \(O(1)\)
C++ code:
#include<iostream>
using namespace std;
signed main() {
int a, b, m;
cin >> a >> b >> m;
int x, y, ans = 0;
for (int i = 0; i * a <= m; i++) {
x = i;
y = (m - x * a) / b;
ans = max(ans, x * a + y * b);
}
cout << ans << endl;
}
Python code:
a, b, m = map(int, input().split())
ans = 0
for i in range(m // a + 1):
ans = max(ans, i * a + (m - i * a) // b * b)
print(ans)
Bu muammo bilan ko'pchilik printerda kitob chiqarmoqchi bo'lganlar to'qnashgan bo'lishsa kerak.
Masala shartida ko'rsatilgani kabi birinchi listni old tarafini ko'radigan bo'lsak, oxirgi hamda birinchi betlar keyingi listda esa mos ravishda 2 ta oldingi va keyingi betlar chop etilgan va shu tartibda davom etilgan.
Orqa tarafini ko'radigan bo'lsak oxirgidan bitta oldingi va 2-sahifalar va keyingi sahifalarda old tarafidagi qonuniyat takrorlangan va bu kitob uchun nechta list kerak bo'lsa shuncha marta takrorlangan.
Nechta list kerakligini topish uchun esa required_lists = (N + 3) / 4 yoki oddiygina ceil(N / 4) formuladan foydalanishingiz mumkin.
Yana bir muammo shundaki: Agar kitobdagi sahifalar soni 4 ga karrali bo'lmagan taqdirda biz uni 4 ga karrali qilib olishimiz kerak aks holda kitob formati buzilib qoladi ya'ni N = required_lists * 4, sababi bir listga 4 sahifa chop etish mumkin.
Shu g'oyani amalga oshirish orqali masalaga osongina yechim topshingiz mumkin
C++ code:
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int required_lists = (n + 3) / 4;
// ceil(n / 4)
n = required_lists * 4;
cout << required_lists << endl;
for (int i = 0; i < n / 4; i++)
{
cout << n - 2 * i << " " << 2 * i + 1 << " ";
}
cout << endl;
for (int i = 0; i < n / 4; i++)
{
cout << 2 * i + 2 << " " << n - 2 * i - 1 << " ";
}
}
Python code:
n = int(input())
required_lists = (n + 3) // 4
# ceil(n / 4)
n = required_lists * 4
print(required_lists)
for i in range(required_lists):
print(n - 2 * i, 2 * i + 1, end=' ')
print()
for i in range(required_lists):
print(2 * i + 2, n - 2 * i - 1, end=' ')
C++ code:
#include<iostream>
using namespace std;
signed main() {
int n;
cin >> n;
int m = 2 * n - 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < m; j++) {
cout << min(abs(i - (n - 1)), abs(j - (n - 1))) + 1 << " ";
}
cout << endl;
}
}
Python code:
n = int(input())
m = 2 * n - 1
for i in range(m):
for j in range(m):
print(min(abs(i - (n - 1)), abs(j - (n - 1))) + 1, end=" ")
print()
C++ code:
#include<bits/stdc++.h>
using namespace std;
signed main(){
int n;
cin >> n;
map<int, int> mp;
for(int i = 0; i < n; i++){
int x;
cin >> x;
mp[x]++;
}
int gcd = 1, a = 1, b = 1;
for(auto i : mp){
a = max(a, i.first);
if(i.second > 1){
gcd = max(gcd, i.first);
}
}
for(auto i : mp){
int x = i.first;
int y = i.second;
if (x % gcd == 0 and __gcd(x / gcd, a / gcd) == 1) {
b = max(b, x);
}
}
cout << a << " " << b << endl;
}
Python code:
import math
n = int(input())
a = list(map(int, input().split()))
mp = {}
for i in a:
if i in mp:
mp[i] += 1
else:
mp[i] = 1
gcd = 1
mx = 1
for i in mp:
mx = max(mx, i)
if mp[i] > 1:
gcd = max(gcd, i)
b = 1
for i in mp:
if i % gcd == 0 and math.gcd(i // gcd, mx // gcd) == 1:
b = max(b, i)
print(mx, b)
C++ code:
#include <bits/stdc++.h>
using namespace std;
int32_t main() {
int t;
cin >> t;
for (int i = 0; i < t; i++) {
string s;
cin >> s;
int a[26] = {0};
int c = 0;
for (char i : s) {
a[i - 'a']++;
}
for (long long i : a) {
if (i % 2 == 1) {
c++;
}
}
if (c == 0) {
cout << "First";
} else if (c % 2 == 1) {
cout << "First";
} else {
cout << "second";
}
cout << endl;
}
}
Python code:
t = int(input())
for i in range(t):
s = input()
a = [0] * 26
c = 0
for i in s:
a[ord(i) - ord('a')] += 1
for i in a:
if i % 2 == 1:
c += 1
if c == 0:
print("First")
elif c % 2 == 1:
print("First")
else:
print("Second")
C++ code:
#include <bits/stdc++.h>
using namespace std;
int L, R, k;
bool check(int x)
{
for (int i = 2; i * i <= x; i++)
{
if (x % i == 0)
return 0;
}
return 1;
}
int find(int x, int y)
{
if (!check(y))
return 0;
int sum = x / y;
for (int i = 2; i <= min(x / y, y - 1); i++)
sum -= find(x / y, i);
return sum;
}
int main()
{
cin >> L >> R >> k;
cout << find(R, k) - find(L - 1, k);
return 0;
}
Python code:
def check(x):
for i in range(2, int(x ** 0.5) + 1):
if x % i == 0:
return False
return True
def find(x, y):
if not check(y):
return 0
s = x // y
for i in range(2, min(x // y, y - 1) + 1):
s -= find(x // y, i)
return s
l, r, k = map(int, input().split())
print(find(r, k) - find(l - 1, k))