Masala #R025C
Daraxtlarni ulash
Daraxt deb bog’langan, \(n\) ta tugun va \(n-1\) ta shoxdan iborat grafga aytiladi.
Sizga mos ravishda \(n\) ta va \(m\) ta tugundan iborat bo’lgan ikkita daraxt berilgan. Birinchi daraxtning biror tugunini ikkinchi daraxtning biror tuguniga ulash orqali bitta yangi daraxt hosil qilindi. Sizning vazifangiz esa hosil bo’lgan daraxtda ixtiyoriy ikkita tugun orasidagi maksimal masofa eng kamida qancha bo’lishi mumkinligini topishdan iborat.
Ikki tugun orasidagi masofa deb, bu tugunlar orasidagi shoxlar soniga aytiladi.
Birinchi qatorda bitta butun \(n\) soni - birinchi daraxt tugunlari soni \((1 ≤ n ≤ 10^5)\). Ikkinchi qatorda esa \(n-1\) ta \(u\) va \(v\) ko’rinishidagi juftliklar, ya’ni birinchi daraxt bog’lanishlari beriladi \((1 ≤ u, v ≤ n, u \ne v)\). Keyingi qatorda esa xuddi shu tartibda ikkinchi daraxt beriladi, dastlab \(m\) butun soni, so’ngra \(m - 1\) ta \(u\) va \(v\) juftliklar \((1 ≤ m ≤ 10^5, 1 ≤ u, v ≤ m, u \ne v)\).
Bitta butun son – masalaning javobi.
| # | input.txt | output.txt |
|---|---|---|
| 1 |
3 1 2 1 3 4 1 2 2 3 2 4 |
3 |
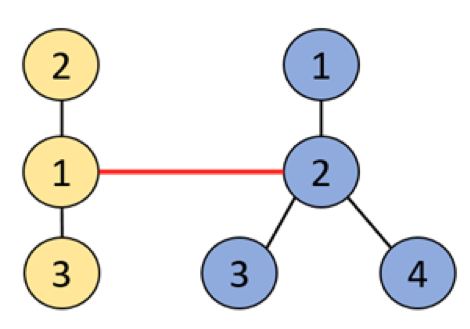
Quyidagi rasmda birinchi daraxt sariq rangda, ikkinchi daraxt ko’k rangda berilgan, ularni bog’lovchi shox esa qizilda berilgan, yangi daraxtdagi eng uzun masofa 3.