Masala #R036B
Fraktal
Asadullo fraktal shakllarga qiziqadi. U yangi fraktal shakl o’ylab topdi va uni quyidagi tartibda to’ldira boshladi:
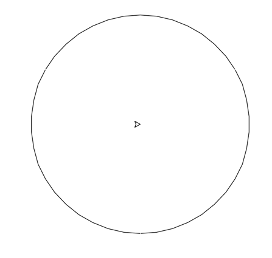
- 1-qadamda Asadullo \(R\) radiusli aylana chizib oldi.
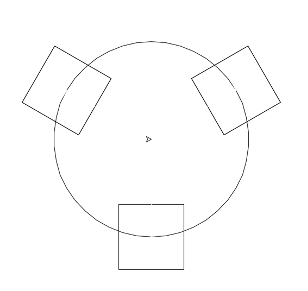
- 2-qadamda 1-qadamda chizilgan aylananing atrofida 3 ta kvadrat chizdi
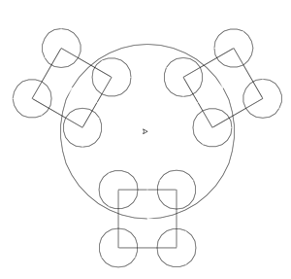
- 3-qadamda 2-qadamda chizilgan kvadratlarning to’rttala qirrasida ham aylana chizdi
- …
- \(2*k\) – qadamda \(2*k-1\) – qadamda chizilgan aylanalarning atrofida 3 tadan kvadrat chizdi
- \(2*k+1\) – qadamda \(2*k\) – qadamda chizilgan kvadratlarning to’rttala qirrasida ham aylana chizdi
- …
|
1-bosqich |
2-bosqich |
3-bosqich |
|
|
|
|
Asadullo ushbu fraktal shaklning \(N\)-qadamigacha chizib chiqish murakkab ekanligini, lekin, \(N\)-qadamgacha jami nechta shakl chizilganini (aylana va kvadratlar) aniqlash mumkinligini tushunib yetdi. Asadulloga \(N\)-qadamgacha chizilgan shakllar sonini aniqlashda yordam bering.
Kirish faylida yagona butun son, \(N(1 ≤ N ≤ 10^{18)}\) soni kiritiladi.
Chiqish faylida yagona son, \(N\)-qadamigacha chizilgan shakllar umumiy sonini \(1000000007(10^9+7)\) ga bo’lgandagi qoldiqni chop eting!
| # | input.txt | output.txt |
|---|---|---|
| 1 |
1 |
1 |
| 2 |
2 |
4 |
| 3 |
3 |
16 |