Masala G
Mukammal jadval
Sizda tomoni \(N\) ga teng bo’lgan jadval bor. Siz esa bu jadvaldan ‘Mukammal’ jadvalni hosil qiling. ‘Mukammal’ jadval bo’lishi uchun 2ta shart bor:
• Uning 4 tomonining uzunligi ham \(N\) ga teng bo'lishi kerak
• Uning har bir katagida \(1\) yoki \(0\) yozilishi shart
Ikki jadvalning har xilligi deb, shu ikki jadval bir-biridan, birini qanchadir gradusga aylantirganda ikkinchisi bilan bir xil bo’lib qolmasligiga aytiladi.
Sizning vazifangiz shundan iboratki, bu \(N\times N\) jadvaldan hosil qilish mumkin bo’lgan har xil ‘Mukammal’ jadvallar sonini toping.
Kirish faylida, bitta butun son N (\(1\leq N\leq10^9\)) beriladi.
Tomoni \(N\) ga teng bo'lgan ‘Mukammal’ jadvallar sonini toping. Bunday jadvallar soni juda katta bo'lib ketishi mumkin, shuning uchun javobni \(10^9+7\)ga bo'lgandagi qoldiqni chop eting.
| # | input.txt | output.txt |
|---|---|---|
| 1 |
2 |
6 |
| 2 |
5 |
8390720 |
| 3 |
9 |
5179184 |
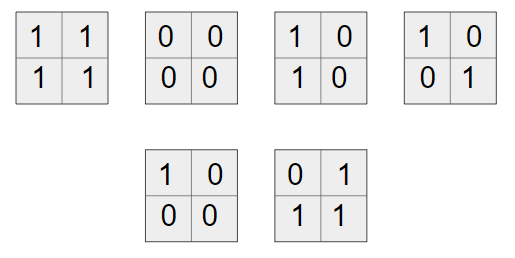
\(N=2\) bo'lganda hosil qilib bo'ladigan mukammal jadvallar: