Masala #M023M
Muhim tugunlar #2
\(N\) ta tugun va \(M\) ta qirradan iborat bog’langan yo’nalmagan graf berilgan. Ya’ni graf qirralari ikki tomonlamali hamda grafdagi ixtiyoriy tugundan boshqasiga qirralar orqali borish mumkin.
\(x\) va \(y\) tugunlar \((x \ne y)\) uchun muhim tugun deb shunaqangi \(u\) tugunga aytiladiki \((u \ne x, u \ne y)\), agar shu \(u\) tugun grafdan olib tashlansa, grafda \(x\) dan \(y\) ga borishni imkoni bo’lmay qolsin.
Sizga \(q\) ta so’rovlar orqali \(x\) va \(y\) tugunlar juftliklari beriladi, har bir so’rovdagi juftlik uchun muhim tugunlar sonini chiqaring.
Birinchi qatorda ikkita butun son tugunlar soni \(n\) va qirralar soni \(m\) kiritiladi \((3 ≤ n, m ≤ 10^5)\). Keyingi \(m\) ta qatorda graf qirralari \(u\) va \(v\) sonlar juftligi ko’rinishida beriladi \((1 ≤ u, v ≤ n, u \ne v)\).
Keyingi qatorda so’rovlar soni \(q\) beriladi \((1 ≤ q ≤ 10^5)\). Keyingi \(q\) ta qatorda so’rovlarni ifodalovchi \(x\) va \(y\) sonlar juftligi beriladi \((1 ≤ x, y ≤ n, x \ne y)\).
1-subtask (11 ball): \(n, m, q ≤ 300\).
2-subtask (9 ball): Graf to’g’ri chiziq shaklida, ya’ni har bir tugunni bitta yoki ikkita qo’shnisi bo’lishi mumkin (\(m = n - 1\) va \(n, q ≤ 10^5\)).
3-subtask (13 ball): \(m = n - 1\) hamda har bir \(i*2+1 ≤ n\) bo’lgan \(i\)-tugundan \(i*2\) va \(i*2+1\) tugunlarga qirra mavjud (\(m = n - 1\) va \(n, q ≤ 10^5\)).
4-subtask (21 ball): \(m = n - 1\) va \(n, q ≤ 10^5\)
5-subtask (46 ball): \(n, m, q ≤ 10^5\)
Har bir so’rov uchun \(x\) va \(y\) tugunlar juftligiga nisbatan muhim bo’lgan tugunlar sonini chiqaring.
| # | input.txt | output.txt |
|---|---|---|
| 1 |
9 14 4 7 5 6 5 7 6 7 1 8 1 2 1 3 3 4 3 5 4 5 1 9 2 9 2 8 9 8 3 3 8 1 3 4 9 |
1 0 2 |
Birinchi misoldagi graf quyidagicha ko’rinishda:
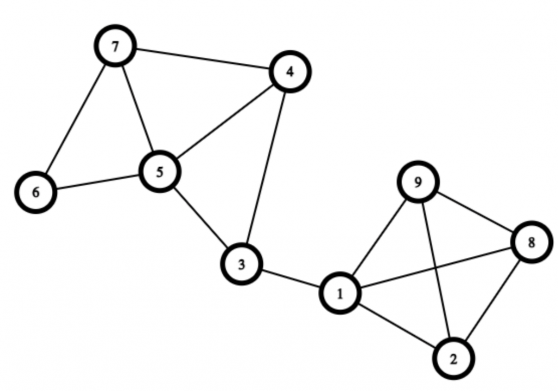
1-so’rovda 3 va 8 tugunlar uchun yagona muhim tugun 1-tugun hisoblanadi.
2-so’rovda 1-va 3- tugunlar uchun birorta ham muhim tugun yo’q, grafdagi boshqa ixtiyoriy tugunni olib tashlasa ham bu tugunlar o’rtasida yo’l doim bo’ladi.
3-so’rovda 4- va 9- tugunlar uchun muhim tugunlar 3- va 1- tugunlardir.