Masala #A0094
Shohruh va mango daraxtlari
Bir kuni Shohruhning g'ayrioddiy tajribalari uchun mango mevalari zarur bo'lib qoldi.Shuning uchun u o'rmonga mango terish uchun yo'l oldi.
Tekislikdagi \((x, y)\) nuqtani ko'rib chiqaylik, x va y butun sonlar va 0 ≤ x, y bo'lsin. Bunday nuqtada daraxt o'sadi, unda x + y mango bor. Boshqa joylarda daraxtlar yo'q. Shohruh \(y = -{x \over m} + b\) tenglama bilan to'g'ri chiziq chizdi. Shohruh tomonlari koordinata o'qlariga parallel bo'lgan bitta to'rtburchakni tanlashi mumkin, uning barcha nuqtalari chiziq ostida yoki chiziqda yotadi va to'rtburchak ichidagi va chegarasidagi barcha daraxtlarni kesib, ulardagi barcha mangolarni yig'adi.
Shohruhga to'rtburchakni optimal tanlasa, olishi mumkin bo'lgan mangolarning maksimal sonini topishga yordam bering.
Shohruh ishonchi komilki, javob \(10^{18}\) dan oshmaydi. Unga ishonishingiz mumkin.
Kirish faylida ikkita butun son m va b sonlari kiritiladi \((1 \le m \le 1000, 1 \le b \le 10000)\).
Chiqish faylida Shohruh kesgan daraxtlardan oladigan mangolarning maksimal sonini chop eting.
| # | input.txt | output.txt |
|---|---|---|
| 1 |
3 6 |
273 |
| 2 |
1 5 |
30 |
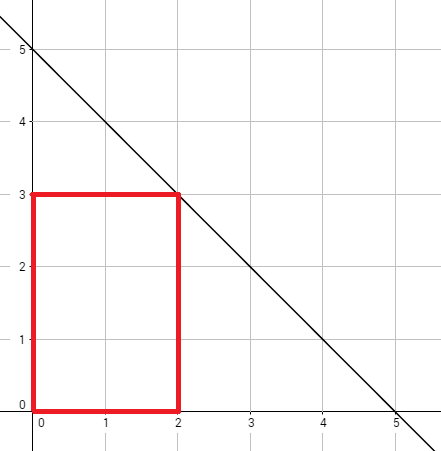
Yuqoridagi rasm ikkinchi misolga mos keladi. Optimal to'rtburchak qizil rangda ko'rsatilgan va 30 ta mangoni o'z ichiga oladi.